A map projection is a systematic transformation of the latitudes and longitudes of locations on the surface of a sphere or an ellipsoid into locations on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. There is no limit to the number of possible map projections. More generally, the surfaces of planetary bodies can be mapped even if they are too irregular to be modeled well with a sphere or ellipsoid. Even more generally, projections are the subject of several pure mathematical fields, including differential geometry and projective geometry. However "map projection" refers specifically to a cartographic projection.
Maps can be more useful than globes in many situations: they are more compact and easier to store; they readily accommodate an enormous range of scales; they are viewed easily on computer displays; they can facilitate measuring properties of the terrain being mapped; they can show larger portions of the Earth's surface at once; and they are cheaper to produce and transport. These useful traits of maps motivate the development of map projections. However, Carl Friedrich Gauss's Theorema Egregium proved that a sphere's surface cannot be represented on a plane without distortion. The same applies to other reference surfaces used as models for the Earth. Since any map projection is a representation of one of those surfaces on a plane, all map projections distort. Every distinct map projection distorts in a distinct way. The study of map projections is the characterization of these distortions.
The Mollweide projection is a pseudocylindrical map projection generally used for global maps of the world (or sky). Also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. As its more explicit name Mollweide equal area projection indicates, it sacrifices accuracy of angle and shape in favor of accurate proportions in area. It is used primarily where accurate representation of area takes precedence over shape, for instance small maps depicting global distributions. The projection was first published by mathematician and astronomer Karl (or Carl) Brandan Mollweide (1774 – 1825) of Leipzig in 1805. It was popularized by Jacques Babinet in 1857, giving it the name homalographic projection. The variation homolographic arose from frequent nineteenth century usage in star atlases.
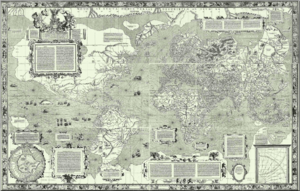
The Mercator projection is a cylindrical map projection presented by the Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as straight segments which conserve the angles with the meridians. While the linear scale is equal in all directions around any point, thus preserving the angles and the shapes of small objects (which makes the projection conformal), the Mercator projection distorts the size and shape of large objects, as the scale increases from the Equator to the poles, where it becomes infinite.
Azimuthal projections have the property that directions from a central point are preserved and therefore great circles through the central point are represented by straight lines on the map. Usually these projections also have radial symmetry in the scales and hence in the distortions: map distances from the central point are computed by a function r(d) of the true distance d, independent of the angle; correspondingly, circles with the central point as center are mapped into circles which have as center the central point on the map. The mapping of radial lines can be visualized by imagining a plane tangent to the Earth, with the central point as tangent point.

Use the information provided on the cache page to solve for the position of the cache container. It can be found 2918.9 meters on an azimuth of 4944 mils from the posted coordinates.
