Einleitung
PPS steht für
Produktionsplanung und -steuerung. Letztlich kennen wir alle die
interessanten Beiträge aus "Die Sendung mit der Maus" oder
"Galileo", in denen erklärt wird, wie alltägliche Produkte
hergestellt werden. Dieser Cache zeigt einige Planungsprobleme in
diesem Rahmen auf und soll dazu anregen, sich einmal mit
produktionswirtschaftlichen Fragen zu beschäftigen. Dazu teilt sich
der Cache in zwei Arbeitsschritte:
- Zu jeder
Station dieses Multi-Caches gibt es ein Planungsproblem. Dieses
kann von zu Hause bequem mittels Recherche im Netz und ein bisschen
Mathematik gelöst werden. Die Aufgaben sind so gehalten, dass sie
durch Nachdenken und geschicktes "Hinsehen" berechnet werden
können.
- Mit den Ergebnissen aus Teil 1 geht es nun vor Ort in den Wald
in der Nähe von Stommelerbusch. Die beste Parkmöglichkeit liefern
die angegebenen Koordinaten. Dort angekommen müssen die Stationen
abgelaufen werden, um schließlich die Cache-Koordinaten zu
berechnen. Die Strecke ist dabei ca. 5,5 km lang und man ist
stellenweise gezwungen, auf einem Reitweg zu laufen.
Ein Taschenrechner ist bei den Berechnungen der Koordinaten
dringend erforderlich ("%" steht dabei für Modulo und Punktrechnung
geht vor Strichrechnung)!
Teil 1: Vorbereitung am
Schreibtisch
Standortplanung
Lösung: A
=
Aufgabe:
Stellen wir uns vor, wir wären Unternehmer eines mittelständischen
Produktionsunternehmens und würden unsere Abnehmer und deren Bedarf
kennen. Für diese Abnehmer wollen wir einen oder mehrere
Produktionsstandorte eröffnen, die sie beliefern (Hinweis: Ein
Abnehmer kann von mehreren Standorten beliefert werden). Hierzu
sind uns vier potentielle Standorte gegeben, aus denen wir
auswählen müssen. Mit der Eröffnung eines Standortes sind Fixkosten
verbunden und jeder Standort hat nur eine maximal verfügbare
Kapazität. Darüber hinaus entstehen bei der Belieferung pro
Mengeneinheit Transportkosten in Abhängigkeit von der
Entfernung.
Wir suchen nun die gesamtkostenminimale Lösung, bei der der Bedarf
aller Abnehmer befriedigt wird. Diese Lösung sei A.
Folgende Daten sind gegeben:
Bedarfsmengen und Produktionskapazitäten
| Abnehmer |
potentielle
Produktionsstandorte |
| Ort |
Bedarfsmenge |
Ort |
Kapazität |
| Hamburg |
200 |
Dortmund |
500 |
| Berlin |
170 |
Bremen |
700 |
| München |
230 |
Karlsruhe |
700 |
| Köln |
220 |
Passau |
500 |
Transportkosten je Mengeneinheit
| Von/nach |
Hamburg |
Berlin |
München |
Köln |
| Dortmund |
344 |
500 |
608 |
92 |
| Bremen |
120 |
392 |
748 |
323 |
| Karlsruhe |
630 |
686 |
277 |
311 |
| Passau |
826 |
638 |
195 |
630 |
Sonstige Daten
Fixkosten für
die Eröffnung eines Standortes: 50000 Geldeinheiten
Nachfrageprognose
Lösung: B
=
Aufgabe:
Aus unserer bisherigen Geschäftstätigkeit kennen wir die Nachfragen
aus den letzten 6 Jahren. Wir wollen nun die Nachfrage für das
nächste Jahr prognostizieren. Hierzu nutzen wir die exponentielle
Glättung erster Ordnung (der Glättungsparameter sei 0,2 und der
Prognosewert für die erste Periode sei gleich dem Beobachtungswert
der ersten Periode). Der sich dabei ergebende, aufgerundete
Prognosewert sei B.
Folgende Daten sind gegeben:
Nachfragemengen
| 1. Jahr |
2. Jahr |
3. Jahr |
4. Jahr |
5. Jahr |
6. Jahr |
| 492 |
504 |
477 |
494 |
489 |
502 |
Losgrößenplanung
Lösung: C
=
Aufgabe:
In unserem nächsten Problem stecken wir schon mitten in der
eigentlichen Produktion. Wir kennen die Bedarfsmengen der nächsten
fünf Perioden und wollen sie produzieren. Aber wann? Am liebsten
würden wir in jeder Periode den entsprechenden Bedarf herstellen.
Das Problem dabei ist, dass mit der Produktion Rüstkosten verbunden
sind (z. B. Kosten für Reinigungsmaterial). Aus diesem Grund sind
wir gezwungen, Periodenbedarfsmengen zu Losen zusammenzufassen,
d.h. wir produzieren Bedarfsmengen im voraus. Letzteres bedingt,
dass wir die Bedarfsmengen zukünftiger Perioden lagern müssen.
Dafür entstehen Lagerkosten in Abhängigkeit der Menge und der Zeit.
Wir müssen nun abwägen zwischen Lager- und Rüstkosten. Dabei
verfolgen wir natürlich das Ziel, die kostengünstigste Lösung zu
finden unter der Voraussetzung, dass alle Bedarfsmengen
termingerecht spätestens in der Periode ihres Auftretens produziert
werden. Die Kosten dieser Lösung seien C.
Folgende Daten sind gegeben:
Bedarfsmengen
| 1. Periode |
2. Periode |
3. Periode |
4. Periode |
5. Periode |
| 40 |
53 |
47 |
56 |
49 |
Sonstige Daten
Rüstkosten
pro Periode, in der produziert wird: 200 Geldeinheiten
Lagerkosten pro Mengeneinheit und Periode: 4
Geldeinheiten
Warteschlangentheorie
Lösung: D
=
Aufgabe:
Wir wissen, dass unsere Produktion pro Arbeitstag 100 Einheiten
eines Erzeugnisses fertig stellt und dass die mittlere
Fertigungsdurchlaufzeit (d. h. die Zeit vom Beginn eines
Fertigungsauftrags bis zu dessen Fertigstellung) 15 Arbeitstage
(drei Wochen) beträgt. Wie hoch ist der Bestand an angearbeiteten
Aufträgen? Dieser Wert sei L1.
Wir wissen weiterhin, dass ein Fertigungsauftrag von den 15
Arbeitstagen sich 14 Tage in Wartestatus auf die nächste
Bearbeitung befindet. Wie viele Aufträge warten im Mittel innerhalb
des Fertigungsbetriebes auf ihre Weiterverarbeitung? Dieser Wert
sei L2. Der Wert für D ergibt sich nun aus der Summe
von L1 und L2.
Durchlaufterminierung
Lösung: E
=
Aufgabe:
In unserem letzten Arbeitsschritt kümmern wir uns um die
Durchlaufterminierung. Dabei sind uns die Arbeitsgänge, deren
Bearbeitungsdauer und die Vorgänger-Nachfolger-Beziehungen bekannt.
Wir wollen nun bestimmen, wann die einzelnen Arbeitsgänge
frühestmöglich und spätestmöglich begonnen und beendet werden
können. Hierzu verwenden wir einen MPM-Netzplan
(Vorgangs-Knoten-Netzplan). Mittels Vorwärts- und
Rückwärtsterminierung ermitteln wir die Pufferzeit eines jeden
Arbeitsganges (d.h. die Zeit, die ein Arbeitsgang zeitlich
vorgezogen oder in die Zukunft verschoben werden kann, ohne einen
nachfolgenden Auftrag hinsichtlich seiner Zeitplanung zu
beeinflussen). Zeitliche Mindestabstände zwischen den Arbeitsgängen
müssen nicht berücksichtigt werden. Die Summe der Pufferzeiten
aller Arbeitsgänge sei E.
Folgende Daten sind gegeben:
Graphen zum Eintragen der Ergebnisse
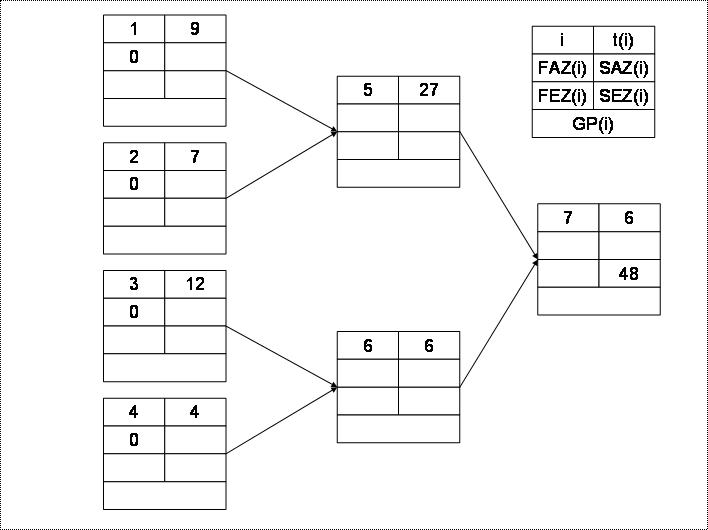
Legende
- i = Nummer
des Arbeitsganges
- t(i) = Bearbeitungsdauer von Arbeitsgang i
- FAZ(i) = frühestmöglicher Anfangszeitpunkt von Arbeitsgang
i
- FEZ(i) = frühestmöglicher Endzeitpunkt von Arbeitsgang i
- SAZ(i) = spätestmöglicher Anfangszeitpunkt von Arbeitsgang
i
- SEZ(i) = spätestmöglicher Endzeitpunkt von Arbeitsgang i
- GP(i) = Pufferzeit von Arbeitsgang i
Lösungskontrolle
Ich würde
Euch gerne ersparen, ggf. mit falschen Ergebnissen vor Ort auf die
Suche zu gehen. Aus diesem Grund biete ich Euch eine Überprüfung
der Ergebnisse per Mail an. Schreibt dazu einfach eine Mail an
A_B_C_D_E@gmx.de (z.B. 5123_466_22143_543_22@gmx.de). Falls Eure
Ergebnisse richtig sind, bekommt Ihr eine automatische
Antwortmail.
Teil 2: Auf in den Wald
1. Station
Koordinaten:
N 51° 3.((abgerundet(Wurzel(A)))-270) E 6°
46.((A%1000)+75)
Lösung: F
=
Aufgabe:
Hier befindet sich ein Tor. Wie viele diagonale Streben hat es? Die
Anzahl sei F.
2. Station
Koordinaten:
N 51° 3.((B%100)*F*(F-1)+16) E 6° 47.(B-F*108-1)
Lösung: G
=
Aufgabe:
An dieser Stelle ist ein Mikro versteckt. In diesem findet sich
eine Frage zur obigen Aufgabe zum Thema "Warteschlangentheorie". Es
geht dabei um die in der Aufgabe abgefragten mathematischen
Zusammenhänge. Der Wert der richtigen Lösung sei G.
Kann die Frage nicht beantwortet werden, dann besteht die
Möglichkeit durch Anlaufen einer Zusatzstation, den notwendigen
Wert zu erfahren. Näheres hierzu im Mikro!
3. Station
Koordinaten:
N 51° 3.(C-20*G+8) E 6° 47.(C/2+G+E-3)
Lösung: H
=
Aufgabe:
Hier steht ein Baum mit einer Aufschrift. Diese besteht aus zwei
Buchstaben, die weit im Alphabet auseinander liegen, und einer
Zahl. Die Zahl sei H.
4. Station
Koordinaten:
N 51° 3.(D/10*2-H*4-2) E 6° 47.(D-H*H*4+108)
Lösung: I
=
Aufgabe:
An den Koordinaten ist, ein Schild zu finden. Auf diesem findet
sich eine Zeitangabe für eine Weglänge. Nehmt hier die
Minutenangabe (die Stundenangabe ist zu vernachlässigen) und
addiert die Zahl, die sich auf dem Schild hinter dem ersten
Buchstaben des Alphabets findet. Die Summe sei I.
5. Station
Koordinaten:
N 51° 2.((I*I+E)*3-46) E 6° 47.(E*7+I*4+10)
Lösung: J
=
Aufgabe:
An der letzten Station steht ein Metallobjekt. Auf dem Deckel
stehen Buchstaben. Bilde die Summe der Buchstaben (d.h. A=1, B=2,
C=3 usw.), welche J sei.
Cache-Location
Koordinaten:
N 51°
2.abgerundet(Wurzel(A+B*B+C*95+D*100+E*E+F*F+G*G+H*H+I*I+J*J)) E 6°
47.(C-B-G*3-H-I-F*4-J)
Im Cache sollten bleiben:
Logbuch
Bleistift
Viel
Erfolg!!!