GC4N6QJ Cyphras (Unknown Cache) in Sachsen-Anhalt, Germany created by MaJu1712 (adoptiert von sax76)

This cache has been archived.

MaJu1712: Aufgrund der örtlichen Gegebenheiten ist hier Schluss.
Dosen im Müll suchen, das wollen wir niemandem antun.
Sorry

GC4N6QJ ▼

A cache by MaJu1712 (adoptiert von sax76) Message this owner

Hidden : 9/12/2013

Difficulty:

Terrain:

Size: Size: small (small)

Join now to view geocache location details. It's free!

Watch

How Geocaching Works

Please note Use of geocaching.com services is subject to the terms and conditions in our disclaimer.

Geocache Description:

Don't Panic, zum lösen braucht man keine höhere Mathematik!

Ja, ich wollte auch mal wieder einen Mystery ins Feld werfen, nur was für einen? ich überlegte hin und her. Irgendwas mit Mathe sollte es schon sein, aber auch nicht allzu schwer. Die erste Idee war irgendwas mit Fourier-reihen

$f(t)=\frac{a_0}{2} + \sum_{k=1}^\infty (a_k \cdot \cos(k \omega t) + b_k \cdot \sin(k \omega t)).$

Aber dann dachte ich mir, doch lieber nicht, ich mache lieber was mit Polynomen .. Polynome ... was kann man mit Polynomen denn so schönes anstellen? Mach ich erst mal ein Brainstorming: Was fällt mir zu Polynomen ein? Als erstes brauchen wir die Definition

In der elementaren Algebra ist eine Polynomfunktion eine Funktion $P$ der Form

$P(x) = \sum_{i=0}^n a_ix^i = a_0 + a_1x+ a_2x+ \dotsb + a_{n-1}x^{n-1} + a_nx^n , \quad n \ge 0$ ,

wobei als Definitionsbereich für die Variable $x$ jede beliebige $R$ -Algebra in Frage kommt, wenn $R$ der Wertebereich der Koeffizienten ist. Häufig ist dieser jedoch die Menge der ganzen, der reellen oder der komplexen Zahlen.

Vielleicht doch besser ein Beispiel? Hier haben wie ein Polynom 5. Grades.

Nun gut. Was gibt es zu Polynomen noch zu sagen. Polynome bilden, zusammen mit der Addition und der Multiplikation einen Ring, eine algebraische Struktur! Hä was? Genau: Moment, ich krame mal meinen alten "lineare Algebra" Order raus.

Damit sollte alles klar sein. Der Ring der Polynome also. Ob er wohl so aussieht?

Nach all der Theorie erst mal noch ein Beispiel. Hier haben wir ein weiteres Polynom 5. Grades:

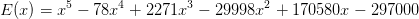
Was fällt mir noch ein. Na klar, Polynome bilden einen Vektorraum, genauer gesagt einen Hilbertraum. Oder doch nur einen Prä-Hilbertraum? Bin mir gerade nicht sicher, aber egal, zumindest gibt es einen ganzen Zoo von Polynomen die "senkrecht" aufeinanderstehen. "Senkrecht" bedeutet dabei, dass man ein Skalarprodukt zwischen Polynomen definiert, wenn dieses für zwei Polynomen verschwindet sind die Polynome zueinander orthogonal. Ist genau wie bei Vektoren, nur halt mit Polynomen. Ist doch ganz einfach oder?

Probieren wir das doch mal mit unseren Beispielen. Das Skalarprodukt zwischen zwei Polynomen P und Q sei definiert als:

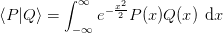
Setzen wir N(x) und E(x) ein finden wir:

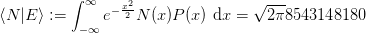
Naja, war ja auch nicht zu erwarten das gerade die beiden orthogonal zueinander sind. Vollständige Sätze Orthogonaler Polynome gibt es jedoch viele, sogar unendlich viele.

Da wären zum Beispiel die Laguerre-Polynome, die wiederum wichtig sind wenn man die Energieniveaus des Wasserstoffatoms ausrechnen will. Die hermitschen Polynome braucht man hingegen zur Beschreibung des Quantenmechnischem harmonischen Oszillators. Da diese Polynome "senkrecht" aufeinander stehen, sind sie hervorragend geeignet um als Basis des Hilbertraums zu dienen. Das ist genauso wie mit der x,y und z Richtung bei Vektoren, nur halt mit Polynomen. Übrigens haben die Anfangs erwähnten, verschiedenen Glieder der Fourierreihe die selbe Eigenschaft, sie stehen "senkrecht" aufeinander und eignen sich hervorragend als Basis für den Raum der periodischen Funktionen. Vielleicht mach ich doch mal irgend was mit Fourier. Aber dies mal nicht, hier gehts um Polynome. Habe ich den Fundamentalsatz der Algebra eigentlich schon erwähnt? Nicht? Egal ...

Ihr wisst nun schon alles was nötig ist um den Cache zu finden. Viel Spaß dabei!