Šrouby a šroubky
Podíváme se do Krupky, resp. do její části Vrchoslavi, kde již 110 let vyrábí spojovací materiál továrna odjakživa nazývaná „šroubárna“. Po roce 1989 na rozdíl od řady i věhlasných českých strojírenských podniků nezanikla. Možná proto, že je na okraji města a že je tak hezky schovaná před „podnikateli“, kterým šlo jen o rychlé zbohatnutí...
V roce 1910 pánové Gerhardt & Rahm založili továrnu na šrouby a tažené železo, a. s., Krupka 1910-1923. Pak továrna nepřetržitě vyráběla pod různými názvy: Gerhardt & Rahm, továrna na šrouby a tažené železo, a.s., Vrchoslav 1923-1945; Pod národní správou 1945-1946; Spojené ocelárny, n. p. Kladno 1946-1949; Drátovny a šroubárny, n. p. závod Vrchoslav 1949-1950; Vrchoslavská šroubárna, n. p. Krupka 1951-1958; VHJ Libčice, závod 03 Krupka 1958-1965; Šroubárna Turnov, provozovna Krupka 1965-1968; GŘ Hutní druhovýroba Praha, podnik Šroubárna Krupka 1969. V roce 1994 zakoupila v rámci privatizace firma ŠROUBY Krupka s. r. o. bývalý státní podnik Šroubárna Krupka a od té doby působí na trhu se spojovacím materiálem. Produkce navazuje na devadesátiletou tradici výroby šroubovacího zboží v podniku a je dnes orientována především na přesné a speciální výrobky s vyšší pracností. Vyráběný sortiment obsahuje šrouby, matice, čepy, kolíky apod. podle norem, ale hlavní náplní jsou přesné výkresové součásti.
Tímto úvodem nechci dělat žádnou reklamu této firmě. Šlo mi jen o to nějak zdůvodnit, že jsem umístil keš zrovna nedaleko vrchoslavské šroubárny. Mám dojem, že když si půjdete do železářství koupit pár šroubků, vrutů, matek nebo podložek, tak vás asi nezajímá, kde byly vyrobeny. Ostatně vruty (šrouby do dřeva), o kterých bude dále řeč, tato firma ani nemá v nabídce.
O přejímkách
Když se něco dělá, tak se to má dělat pořádně. A protože lidé pořádní nebývají, tak se výsledky jejich práce musí kontrolovat. Zdálo by se, že nejlepší způsob kontroly je stoprocentní kontrola, která odhalí každý zmetek. Bohužel vyráběné objemy zboží jsou často tak velké, že to prostě nejde. Někdy je v zájmu co největší produkce zboží v co nejkratším čase výhodnější připustit určité procento vadných výrobků, které jsou odhaleny až v návazných procesech. Nyní se tomu říká „řízení jakosti“ a využívá se při tom metod matematické statistiky.
Zaměřím se jenom na dodavatelsko-odběratelské vztahy. Výrobce (dodavatel) ví, že i přes jeho kontrolní mechanizmy je určité procento jeho výrobků vadných. Odběratel to ovšem ví taky a tak je potřeba, aby mezi nimi došlo k určitému kompromisu co se týče požadavku odběratele na jakost a nízkou cenu a na druhé straně snahy dodavatele co nejvíc zboží co nejdráž prodat. Pokud není možné udělat stoprocentní přejímku, tak se musí z celé dodávky zboží vybrat určitý menší soubor a ten pak podrobit důkladné (stoprocentní) kontrole. Leckdy i destruktivní, jako např. při zkoušení pevnosti šroubů nebo vrutů v tahu, krutu apod.
Teorie přejímek jako matematicko-statistický obor je spjata s obdobím 2. světové války. Během ní bylo potřeba vymyslet nějaký šikovný způsob, jak testovat kvalitu (resp. funkčnost) střeliva s co nejnižšími náklady. Otestovat celou dodávku nábojů nebo granátů na střelnici je samozřejmě nesmysl. Britský matematik H. F. Dodge právě včas předložil svoji teorií přejímek. Stanovil základní výpočetní postupy kontrol založené na teorii pravděpodobnosti a aplikoval je do průmyslové praxe. V r. 1941 na něj navázal Romig v aplikacích pro válečný letecký průmysl. Za války to samozřejmě bylo přísně utajeno. Jejich myšlenky však platí dodnes a platné normy z nich vycházejí a dále je rozvíjejí.
Základním rozdělením přejímek je dělení na přejímky měřením (měří se nějaké parametry) a srovnáváním (výsledkem je verdikt vyhověl nebo nevyhověl. Mohou to být i měřitelné veličiny, ale ty také buď splňují nějaké kritérium, nebo ne). V současnosti existují normy, které obsahují příslušné tabulky a podrobné návody k provádění přejímek. Existuje více způsobů přejímek (jedním, dvěma nebo více výběry nebo postupným výběrem), ale to si najděte v literatuře.
Jak najít keš
Bude to zase jednou mysterka a jako vždycky bude stylová.
První úloha:
Šrouby, matky a vruty patří mezi základní spojovací materiál. Vedení našeho truhlářského podniku dostalo nabídku jisté šroubárny, která nabízí údajně vyšší kvalitu šroubů a vrutů za nižší ceny, než je v kraji obvyklé. Samozřejmě hned nepodepíšeme kontrakt na milióny šroubků neznámé kvality, ale nabízené výrobky si napřed otestujeme. Pro začátek objednáme 3000 vrutů. K tomu účelu navrhneme přejímací plán. Budeme postupovat podle tabulky A (postup A) z ČSN ISO 2859-2. Základem plánu je určení velikosti výběru. V tabulce A této ČSN (klikněte sem) nalezneme v levém sloupci příslušný rozsah celé dodávky (3000 kusů) a v horním řádku hodnotu nepřípustné úrovně jakosti LQ (Limiting Quality) v procentech. Výrobce sice tvrdí, že dodává své zboží v superkvalitě a že jeho přípustná úroveň jakosti AQL (Acceptance Quality Limit – v podstatě průměrná zmetkovitost v delším časovém úseku) je u těchto vrutů sotva čtvrt procenta, ale my se řídíme zásadou „důvěřuj, ale prověřuj“ a tak se pro začátek spokojíme s LQ = 3,15 % zmetků. Do testu z obdržené dodávky 3000 vrutů náhodně vybereme n vrutů; číslo n nalezneme v tabulce A v průsečíku příslušného řádku a sloupce LQ pro hodnotu 3,15 % a rovněž tam uvidíme hodnotu Ac.
Kolik vrutů budeme kontrolovat podle tohoto přejímacího plánu a kolik jich může být (při této kontrole) nanejvýš vadných, aby byla dodávka přijata? Zjištěné hodnoty dosaďte do vzorce pro výpočet souřadnic finálky za n1 a Ac1.
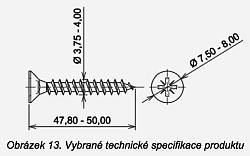Pak pořádně zkontrolujeme oněch vybraných n vrutů. Měříme u nich několik jejich rozměrů, zda jsou v toleranci příslušné ČSN 02 1824 pro toto provedení vrutů (obrázek vlevo) a dále ukazatele kvality jejich zpracování: vizuálně hodnotíme např. špatný závit, ohnutí dříku, zdeformovanou hlavičku nebo špatnou křížovou drážku pro šroubovák PZ2 atd. Výsledkem zkoumání každého testovaného vrutu je zhodnocení vyhovující nebo nevyhovující. Takto zkontrolujeme všech n vrutů a výsledky si pečlivě zapíšeme. Pokud po kontrole všech n vrutů je počet zmetků nižší než hodnota Ac nebo rovný Ac, pak celou dodávku 3000 ks přijmeme. Zmetkovitost by pak měla být maximálně 3,15 %. V průběhu další výroby uvidíme, kolik zmetků vlastně celá dodávka obsahovala a podle toho se zařídíme. Pokud budeme spokojeni, pak můžeme pokračovat s tímto dodavatelem. Samozřejmě i jeho další dodávky aspoň občas zkontrolujeme, zda se jejich kvalita časem nezhoršuje (k tomu ovšem slouží jiné postupy, viz ČSN ISO 2859-1). Pokud ale náš test dopadl špatně (počet nevyhovujících byl vyšší než číslo Ac), tak ta firma bude mít smůlu.
Koho trochu zajímá počet pravděpodobnosti a matematická statistika (doufám, že se snad někdo takový najde...), tak si může přečíst tuto pasáž:
Z výše uvedeného by se mohlo zdát, že přejímky jsou vlastně velmi jednoduchou záležitostí. Stanovíme přejímací plán, z tabulek zjistíme velikost kontrolního souboru n a náhodně vybereme n výrobků, ty zkontrolujeme a pak už jen spočítáme vadné výrobky. Pokud je jejich počet nižší nebo rovný hodnotě Ac (někdy se užívá symbolu c), tak dodávku přijmeme, když je vyšší, tak ji odmítneme, případně budeme v rámci reklamace jednat o slevě. Jenže asi tušíte, že to nebude tak jednoduché; jinak bych o tom určitě nepsal...
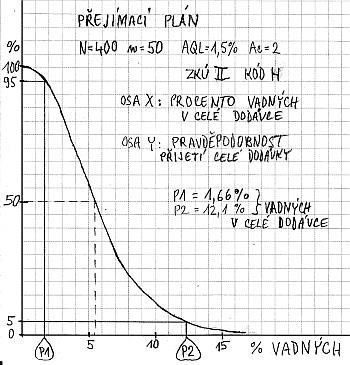Hlavní potíž spočívá v tom, že u konkrétní dodávky neznáme skutečný počet vadných výrobků. Podívejte se na obrázek vlevo: Jde o dodávku 400 atypických vrutů, při čemž chybovost deklarovaná výrobcem (přípustná úroveň jakosti AQL) je údajně 1,5 %. Přejímací plán „H“ má podle ČSN ISO 2859-1 hodnoty n = 50 a Ac = 2. Zkontrolujeme tedy 50 náhodně vybraných vrutů a pokud je počet vadných vrutů vyšší než Ac, tak dodávku odmítneme. Z grafu operativní charakteristiky tohoto přejímacího plánu (vlevo, kliknutím na něj si ho můžete zvětšit) zjistíme, že pokud bude skutečné procento vadných v celé dodávce P1 = 1,66 % (tj. prakticky shodné s AQL), tak bude dodávka přijata s 95% pravděpodobností. To ovšem znamená, že 5 % dodávek (tj jedna z dvaceti) nemusí projít, protože ve výběru budou čirou náhodou 3 nebo více vadných vrutů. To je riziko dodavatele (alfa – zde 5 %). Naopak pokud by bylo v celé dodávce P2 = 12,1 % vadných vrutů (tj. 8x víc než deklaruje dodavatel – pak by ovšem jeho údaj AQL = 1,5 % u této dodávky neodpovídal skutečnosti), tak v 95 % (v 19 výběrech z 20) budou v tomto vybraném souboru 3 nebo více zmetků a celá dodávka 400 vrutů proto bude správně odmítnuta. Ale v 5 % případů se může stát, že se do výběru 50 ks dostanou pouze 2, 1 nebo dokonce žádný vadný vrut a celá dodávka se přijme! Tomu se říká riziko odběratele (beta – v našem případě jsem ho zvolil také 5 %). Sami si můžete z grafu zjistit, že při podílu vadných vrutů P = 5,3 % budou pravděpodobnosti přijetí i odmítnutí dodávky stejné, tj. 50%.
Proto by se měly izolované dodávky s neznámým procentem zmetků nebo od nového dodavatele kontrolovat podle ČSN ISO 2859-2 (tj. podle LQ – viz předešlá úloha), zatímco opakované dodávky od stejného dodavatele stačí hodnotit podle ČSN ISO 2859-1 (podle AQL – viz druhá úloha).
Druhá úloha:
Stanovte přejímací plán pro kontrolu této dodávky: od spolehlivého dodavatele jsme obdrželi už několikátou dodávku, tentokrát 140 000 vrutů určitého provedení. Přípustnou úroveň jakosti AQL dodavatel deklaruje ve výši 2,5 %. Máme s ním dobré zkušenosti, bereme od něj zboží opakovaně a tak není důvod mu nevěřit. Ale pořádek dělá přátele, takže kontrola bude. V tabulce č. 1 z ČSN ISO 2859-1 (klikněte sem) nebo v totožné tabulce z ČSN 01 0254 zjistěte kódové písmeno pro základní kontrolní úroveň II pro velikost celé dodávky. Pak se podívejte do tabulky 2-A téže normy (klikněte sem) a v příslušném řádku vyhledejte kódové písmeno (zjištěné z tab. 1) a rozsah výběru n a v záhlaví příslušného sloupce hodnotu AQL (= 2,5 %). V průsečíku zvoleného řádku a sloupce najděte hodnotu Ac (číslo vlevo; opakuji, že Ac je ještě povolený počet vadných vrutů ve výběru. Re (číslo vpravo) představuje už nepovolený počet zmetků).
Kolik vrutů budeme kontrolovat podle tohoto přejímacího plánu a kolik jich může být (při této kontrole) nanejvýš vadných? Zjištěné hodnoty dosaďte do vzorce pro výpočet souřadnic finálky za n2 a Ac2.
Zjištěné hodnoty dosaďte do vzorce: n1 * Ac1 * n2 * Ac2 / 7
a z výsledku vypočtěte druhou odmocninu. Tím dostanete číslo ABCDEFGH.
Desetinné čárky si nevšímejte a číslici H nezaokrouhlujte. Pak už jen dosaďte:
N 50° (40.509 + 0.EHC)´ E 13° (49.701 + 0.GFD)´
Ještě kontrola:
... a je to!
Poznámky
-
Všechny příklady jsou vymyšlené a slouží pouze k vysvětlení této problematiky.
-
Písmeno n jsem podtrhl jen kvůli zvýraznění. Znamená počet výrobků vybraných ke kontrole. Naproti tomu N značí počet výrobků v celé dodávce.
-
Zobrazené tabulky z několika ČSN slouží pouze k vysvětlení probíraného tématu ve smyslu autorského zákona. Nelze je využívat pro komerční účely.
Obrázek a fotografie owner, jenom třetí obrázek (označený jako Obrázek 13) jsem převzal z diplomové práce Bc. J. Vyškovského.
-
Literatura a odkazy:
Normy ČSN 01 0254 (1974), ST SEV 548-77, ČSN ISO 2859-1, ČSN ISO 2859-2, ČSN 02 1824.
Vyškovský, J.: Statistická přejímka. Dipl. práce VUT Brno, 2010
Reisenauer, K.: Metody matematické statistiky a jejich aplikace. SNTL, Praha 1970
Internet - heslo Přejímky
* * *
Konec
GC8QZQB – verze 1.1 z 28. 2. 2022
(CC BY-SA 3.0 CZ) ladislavappl 2020
