Hamming-Code Mystery Cache
-
Difficulty:
-

-
Terrain:
-

Size:  (small)
(small)
Please note Use of geocaching.com services is subject to the terms and conditions
in our disclaimer.
Der Hamming-Code
In der digitalen Kommunikation gibt es viele Arten der Kodierung, um Informationen zu übertragen. Der Hamming-Code ist ein Code, bei dem eine fehlerhafte Übertragung erkannt und korrigiert werden kann. Hierzu werden den zu übertragenden Daten zusätzliche Bits hinzugefügt.
Die einfachste Variante ergibt sich durch Hinzufügen von zwei Bits zu einem zu übertragenden Datenbit, wobei die zusätzlichen Bits dem zu übertragenden Bit entsprechen. Daher gibt es nur zwei gültige Kodierungen: 000 und 111. Kommt es zu einem Fehler in der Übertragung, so kann durch eine einfache Mehrheitsentscheidung der Fehler korrigiert werden: 101 -> 111.
Effektivere Varianten kommen mit deutlich weniger Kontrollbits aus, die hier verwendete ergänzt 4 Datenbits mit 3 zusätzlichen Bits. Hierzu werden Paritätsbits mit jeweils unterschiedlicher Abdeckung der Datenbits berechnet. Kommt es zu einem Fehler, lässt sich aus den veränderten Paritätsbits auf das fehlerhafte (Paritäts- oder Daten-) Bit eindeutig schließen.
Die Paritätsbits werden wie folgt bestimmt:
p1 ist 1, wenn die Summe der Datenbits d1 + d2 + d4 ungerade ist, ansonsten 0.
p2 ist 1, wenn die Summe der Datenbits d1 + d3 + d4 ungerade ist, ansonsten 0.
p3 ist 1, wenn die Summe der Datenbits d2 + d3 + d4 ungerade ist, ansonsten 0.
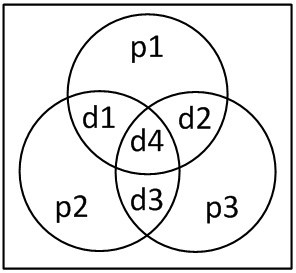
Ist beispielsweise Datenbit d3 bei der Übertragung verändert worden, so sind die Paritätsbits p2 und p3 betroffen.
Um später die Position eines fehlerhaften Bits einfacher bestimmen zu können, werden die drei Bits p1..3 nach folgendem Schema zwischen die Datenbits d1..4 eingefügt: p1, p2, d1, p3, d2, d3, d4.
Beispiel:
Die Daten 0011 (entspricht BCD-codiert dem dezimalen Wert "3") sollen übertragen werden.
p1: Summe der Datenbits d1, d2, d4 (001) = 1 (ungerade) -> 1
p2: Summe der Datenbits d1, d3, d4 (011) = 2 (gerade) -> 0
p3: Summe der Datenbits d2, d3, d4 (011) = 2 (gerade) -> 0
Die zu übertragenden Daten lauten: 1000011
Der Empfänger berechnet die Paritätsbits aus den Datenbits erneut, stimmen sie mit den übertragenen überein ist die Übertragung fehlerfrei erfolgt.
Kommt es zu einem Fehler so sind die berechneten Paritätsbits nicht identisch:
Die empfangenen Daten lauten 1010011, die übertragenen Paritätsbits 100, die berechneten Paritätsbits 010.
Die Bits werden wie oben "exklusiv-oder" verknüpft (Summe ungerade -> 1):
100
010
---
110
Anschließend wird den Bits noch ein Wert zugewiesen: (1 * 1) + (1 * 2) + (0*4) = 3
Das dritte Bit ist fehlerhaft und muss korrigiert werden!
Wer den Hamming-Code verstanden hat, darf sich bei
1001100
0001111
0100101
1110001
1000011
1001000
0100101
1000000
0000000
0001111
1001100
1100110
0101110
1101001
1101110
in das Logbuch eintragen!
Du kannst Deine Lösung bei Geochecker.com überprüfen.
http://de.wikipedia.org/wiki/BCD-Code
http://de.wikipedia.org/wiki/Hamming-Code
Additional Hints
(Decrypt)
Ybpx&Ybpx, zntargvfpu, bora