Edit 2022: I have added English text at the bottom that explains STEP BY STEP how you solve this puzzle, with figures and links.
- The original text by almeidara from 2007 is kept as it is, to respect the history of this old cache.
(Background: When I adopted this cache I did not understand how to solve it. At last I discovered a similar cache in America and the owner Mark McArthur kindly helped me understand how it is done. And it is a bit of work. So I decided to make new figures and put the instructions in the text, so that others can do the same thing. Because the point of mysteries is to learn something new.)
O que é um centro? Um triângulo tem um centro?
Inesperadamente, um triangulo não tem um mas inúmeros centros. Centros são pontos especiais que têm certas propriedades de simetria. Para um circulo, claro que o único ponto totalmente simétrico é o seu centro, mas para uma elipse já podemos ter de considerar os seus dois focos como centros.
Num triângulo temos 4 centros clássicos:
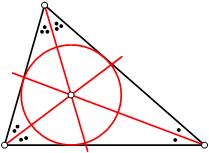
1) incentro: é o centro da circunferência inscrita no triângulo, portanto daquela em que os lados do triângulo são tangentes.
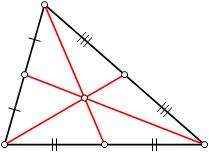
2) baricentro: é a interseção das três medianas. É o centro de gravidade de um triângulo sólido uniforme, o que significa que se pegarmos por um objecto dessa forma a vertical passará sempre pelo ponto onde pegamos e o baricentro. A mediana divide o lado oposto de um vértice ao meio.
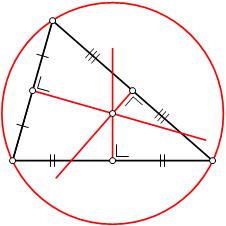
3) circuncentro: ao contrario do incentro, este ponto é o centro da circunferência que inscreve o triângulo. É a interseção das três mediatrizes. Este ponto está portanto a igual distância dos três vertices do triângulo. Definitivamente o mais usado no geocaching  , principalmente porque é o ponto que o GPS acha num triângulo formado pelos satélites na superficie terrestre (embora para ser mais exacto este seja um triângulo esférico). Ver a cache "Na Mouche" (GCMA7E) que faz um excelente uso desta técnica.
, principalmente porque é o ponto que o GPS acha num triângulo formado pelos satélites na superficie terrestre (embora para ser mais exacto este seja um triângulo esférico). Ver a cache "Na Mouche" (GCMA7E) que faz um excelente uso desta técnica.
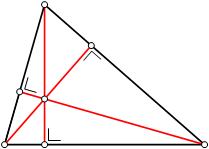
4) ortocentro: É a interseção das tês alturas, rectas que ligam um vertice ao lado oposto num ângulo recto.
Estes eram conhecidos da antiguidade clássica (Gregos). Mais tarde, outros centros foram sendo descobertos (ou inventados, como queiram) como o "centro de nove pontos", "ponto de Lemoine" (ou symmedian point), "ponto de Napolião" ou "ponto de Fermat".
Alguns destes pontos têm propriedades formidáveis. Por exemplo, qualquer que seja o trângulo o ortocentro, o circuncentro, o centróide e o "centro de nove pontos" encontram-se na mesma recta (são colineares)
A internet, essa inesgotável fonte de informação, contém uma enciclopédia com 3248 pontos (@Agosto de 2007) especiais de um triângulo, enumerados desde X(1), X(2) por aí fora. Os primeiros quatro X(n) são os pontos classicos pela ordem descrita a cima. Os primeiros 1200 pontos de Kimberling (criador da enciclopédia):
CACHE
Ok, depois disto tudo só não podia deixar de fazer um pequeno puzzle com isto. A cache encontra-se escondida no "centro de nove pontos" do triângulo definido pelos seguntes pontos:
1) N 38° 35.3899 W 009° 11.9197 (coordenadas publicadas)
2) N 38° 35.6719 W 009° 10.5100
3) N 38° 38.3650 W 009° 10.6239
Agora é só investigar um pouco e fazer uns desenhos num mapa. Considerem o triângulo plano! Fiz a construção que permite obter o ponto pretendido de duas formas distintas. O erro que me deu foi entre 0,5 e 7m, complectamente admissível considerando o erro do sistema GPS.
Podes verificar a solução com uma aproximação de 8m no seguinte link Geochecker.com.
ENGLISH - STEP BY STEP by Hemal
1. The calculator for cincuncenter/orthocenter is outside of "Geocaching toolbox" and uses UTM-format, so first we have to convert the coordinates to UTM-format. Open GeocachingToolbox - "Coordinate conversion", and convert from WGS84 to UTM.
| 1) N 38° 35.3899 W 009° 11.9197 (WGS) => UTM 29S |
482699 |
4271280 |
| 2) N 38° 35.6719 W 009° 10.5100 (WGS) => UTM 29S |
______ |
______ |
| 3) N 38° 38.3650 W 009° 10.6239 (WGS) => UTM 29S |
______ |
______ |
Link: www.geocachingtoolbox.com/index.php?lang=en&page=coordinateConversion
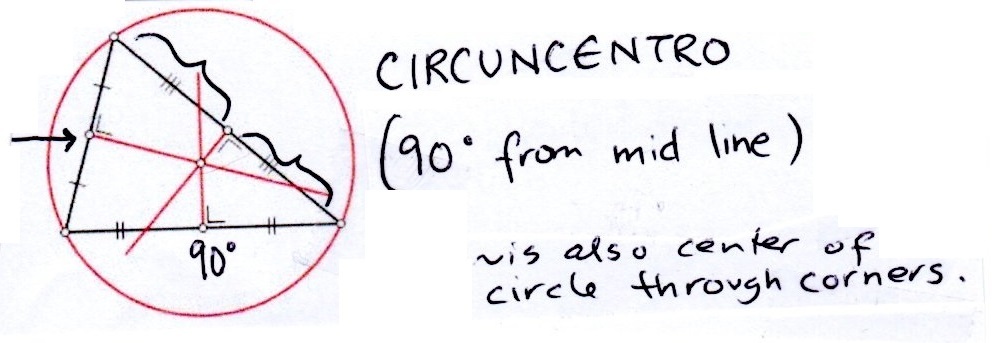
2. Calculate the CIRCUMCENTER in UTM.
The first numbers after "UTM 29S..." is X, the last numbers is Y.
| |
|
X |
Y |
| A) -coordinates 1: |
UTM 29S |
482699 |
4271280 |
| B) -coordinates 2: |
UTM 29S |
_______ |
_______ |
| C) -coordinates 3: |
UTM 29S |
_______ |
_______ |
| CIRCUMCENTER = |
UTM 29S _______ _______ |
Link: scanftree.com/math/calculator/circumcenter-triangle-calculator
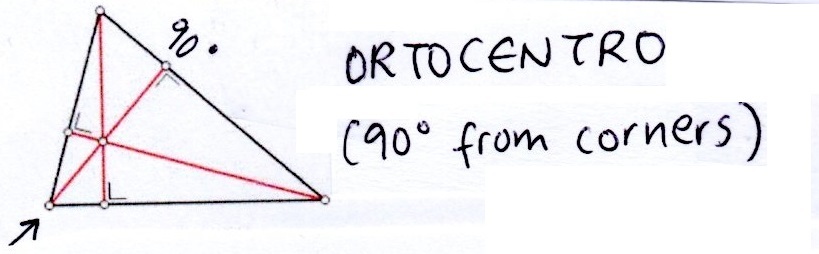
3. Calculate the ORTHOCENTER in UTM
he first numbers after "UTM 29S..." is X, the last numbers is Y.
| |
|
X |
Y |
| A) -coordinates 1: |
UTM 29S |
482699 |
4271280 |
| B) -coordinates 2: |
UTM 29S |
_______ |
_______ |
| C) -coordinates 3: |
UTM 29S |
_______ |
_______ |
| ORTHOCENTER = |
UTM 29S _______ _______ |
Link: scanftree.com/math/calculator/triangle-orthocenter-calculator
4. Now we have calculated two diifferent points in the triangle. And we need to calculate the mid-point between these two points, called the nine-point-center. The calculater is in the Geocaching toolbox, and uses WGS84-format. So we have to convert the two points back to WGS-format:
| |
UTM (remove all decimals) |
WGS84 |
| Orthocenter = |
UTM 29S 48_____ 42_____ |
N 38 _______ W 9 _______ |
| Circumcenter = |
UTM 29S 48_____ 42_____ |
N 38 _______ W 9 _______ |
NB The "S" in "29S" has to be big/capital letter in the calculator!
Link: www.geocachingtoolbox.com/index.php?lang=en&page=coordinateConversion
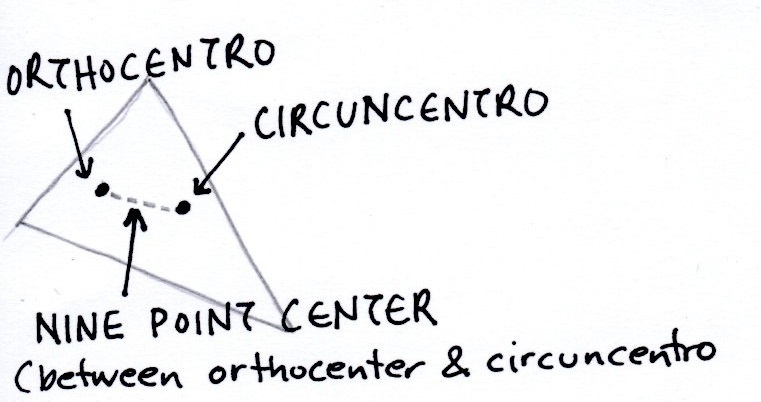
5. No we will calculate the mid-point. That is in Geocaching Toolbox, that uses WGS84-format.
Go to Geocaching toolbox, choose link "Distance, bearing and midpoint":
| Orthocenter = |
N 38 _______ W 9 _______ |
| Circumcenter = |
N 38 _______ W 9 _______ |
| Midpoint / NINE POINT CENTER= |
N 38 _______ W 9 _______ |
Link: www.geocachingtoolbox.com/index.php?lang=en&page=distanceBearingMidpoint
6. Check coordinates on Geochecker.com.
- If you struggle, contact me so I can make the text better. I want people to be able to follow the steps, not to give up. 
EDIT 3.7.2022: Adding english text with links and explanations:
EDIT 19.9.2022: Adding drawings of 3 types of triangles.
EDIT 19.2.2025: Adding tabels and examples in the step-by-step.