|
Deskriptivni geometrie
N 49° 12.401 E 016° 35.553
Kdo nerozumi jednomu pohledu, nepochopi ani dlouhe vysvetlovani.
arabske prislovi
Deskriptivni geometrie je veda o zobrazeni prostorovych utvaru do roviny (prumetny). Podstatou deskriptivni geometrie je jednoznacny vztah mezi zobrazovanym objektem a jeho prumetem (jednim nebo vice). Zjednodusene receno jde o zobrazovani trojrozmernych utvaru na dvojrozmernou nakresnu. Nejzakladnejsi objekty, se kterymi pracuje, jsou body, primky, roviny a uhly. Prakticke vyuziti nasla deskriptivni geometrie vsude tam, kde je treba technicky presne zakreslit ruzne prostorove utvary (strojirenstvi, architektura.).
Technicka praxe vyzaduje v soucasnosti potrebu zobrazovani prostorovych utvaru. Pres soucasny bourlivy rozvoj vypocetni techniky se stale v neztencene mire pouzivaji ve strojirenstvi nebo stavebnictvi plany obsahujici obrazy trojrozmernych utvaru v rovine. Deskriptivni geometrie umoznuje technikum porozumet temto vykresum zobrazenych objektu, je potrebna i pro predstavu budouciho inzenyrskeho dila a jeho zacleneni do okoli.
Znazorneni trojrozmernych objektu je mozne provest dvojim zpusobem:
- Zhotovenim realneho modelu objektu v urcitem zmensenem meritku nebo virtualniho modelu specializovanymi programy. Prednosti tohoto znazorneni je nazornost a srozumitelnost i pro laiky.
- Vyjadreni navrhovaneho objektu pomoci vykresu. Navrh je zpravidla prostorovy utvar a jeho zobrazeni je provedeno utvarem plochy, nejcasteji roviny. Praktickym vysledkem tohoto znazorneni pak je napr. strojni nebo stavebni vykresova dokumentace, mapova dila a dalsi.
Deskriptivni geometrie ma take zvlastni vyznam pri rozvijeni prostorove predstavivosti, schopnosti "prostoroveho videni" a v tribeni logickeho mysleni.
Obsahem deskriptivni geometrie je axiomatika, planimetrie, stereometrie, zobrazovaci metody a konstruktivni geometrie krivek a ploch.
http://cs.wikipedia.org/wiki/Deskriptivni_geometrie
Na uvodnich souradnicich kesku nehledejte, ty vas zavedou na ulici Veveri, pred vstupni branu Stavebni fakulty VUT. V arealu budovy Z, na Zizkove ulici se pak nachazi Ustav matematiky a deskriptivni geometrie, kde se studenti teto fakulty v predmetech AA02 - Deskriptivni geometrie (stud. program Architektura pozemnich staveb), BA03 - Deskriptivni geometrie (stud. program Stavitelstvi) a GA02 - Deskriptivni geometrie (stud. program Geodezie a kartografie) seznamuji ze zaklady deskriptivni geometrie.
Pro uloveni finalky je potreba odpovedet na nasledujici kviz.
Vzhledem k tomu, ze se uz v mem mailboxu objevily e-maily typu, ze keska je jen "tupe googleni" apod., neodpustim si malou poznamku. Ano, je to TEST. Ale co je ucelem testu? Prece OTESTOVAT si vase vedomosti z daneho oboru. Takze je jen na vas, jestli si z lusteni udelate "tupe googleni", nebo jestli se chcete neco noveho a doufam i zajimaveho dozvedet. To zalezi jen a jen va vas. Jestli chcete jen bodik a o deskriptive uz nechcete vubec slyset, tak "tupe googlete", nebo zvazte, jestli se vubec o tuto kesku snazit. Pokud se chcete neco noveho dozvedet, tak zvolte jiny postup.
Kdyz se vas v jedne otazce ptam na stupen jakesi plochy, verim, ze po chvilce vam google vyhodi nejmenovane prednasky, kde se presnou odpoved dozvite. Muzete ale take zvolit jiny postup. Zjistite si nejdrive (treba o par slidu drive), co to vlastne stupen plochy je, a jakym zpusobem se pocita, pote si zjistite, jak je dana plocha urcena a na zaklade toho se muzete sami pokusit zjistit, jakeho stupne pozadovana plocha je.
Kdyz se vas ptam na plochu pouzitou k zastreseni dane budovy, nedelam si iluze, ze nebude problem zadat nazev budovy a k tomu mozne plochy zastreseni a odpoved dostanete. Nebo muzete zvolit postup, kdy si nejdrive vygooglite nebo v literature (jak staromodni...) najdete, jak dane plochy vlastne vypadaji a az pote se podivate na fotografii dane budovy a pokusite se sami urcit o jake zastreseni se jedna.
Takze asi tak k me kesce a ted je na vas, k jakemu zpusobu reseni se rozhodnete. U "tupeho googleni" si ale klidne dve hvezdicky z D uberte. Take je mi jasne, ze pokud se chtel nekdo ucastnit "honu" na xTF, tak asi moc casu na nastudovani latky nemel, vzhledem k tomu, ze padla za tak kratkou dobu.
A) Tecna rovina v nevlastnim bode netorzalni primky n zborcene plochy Φ se nazyva:
1. oskulacni A=1
2. asymptoticka A=2
3. torzalni A=3
B) Plocha Marseillskeho oblouku je stupne:
1. prvniho B=4
2. druheho B=5
3. tretiho B=6
4. ctvrteho B=7
5. pateho B=8
6. sesteho B=9
C) Plocha zadana dvema k sobe kolmymi mimobezkami 1d, 2d a kruznici k lezici v rovine rovnobezne s 1d a 2d a se stredem na ose mimobezek 1d a 2d se nazyva:
1. primy kruhovy konoid C=10
2. plocha sikmeho pruchodu C=11
3. plocha Stramberske truby C=12
4. Kupperuv konoid C=13
5. plocha Montpellierskeho oblouku C=14
D) Meridian rotacni plochy je:
1. rez plochy rovinou prochazejici osou o D=13
2. rez plochy rovinou kolmou k ose o D=12
3. rez plochy libovolnou rovinou D=11
4. rez plochy rovinou rovnobeznou s osou o D=10
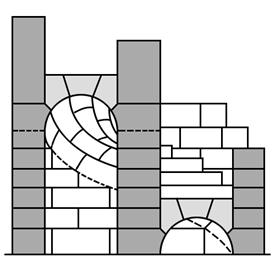
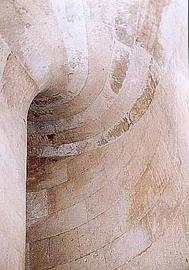
E) Plocha na obrazku se jmenuje:
1. Archimedova serpentina E=9
2. Templarska klenba E=8
3. plocha vinuteho sloupku E=7
4. plocha klenby sv. Jilji E=6
5. plocha klenby srouboveho schodiste E=5
plocha
F) Na dalsim obrazku je zachycena Opera v Sydney od arch. Jorna Utzona. K zastreseni teto budovy bylo uzito trojuhelnikovych useci:
1. rotacniho elipsoidu F=4
2. kulovych ploch o shodnem polomeru F=3
3. hyperbolickeho paraboloidu F=2
4. kruhoveho konoidu F=1
5. trojoseho elipsoidu F=0

Budova Opery v Sydney
G) Jako dosud neokoukany prvek se nektere plochy staly soucasti moderni architektury, ne v pojeti strechy, ale jako esteticky prvek fasady. Z dilny Pei Cobb Freed & Partners pochazi reprezentativni projekty jako Mayerson Symphony Centre (postavene v roce 1989 v Dallasu) a soudni budova v Bostonu z roku 1998. Prosklenne plochy davaji pocit volneho prechodu venkovniho a vnitrniho prostoru. Pricemz na obrazku pouzitou plochou je:
1. elipsoid, G=1
2. hyperboloid G=3
3. konoid G=5
4. valcova plocha G=7

Mayerson Symphony Centre
H) Dalsim krasnym prikladem pouziti plochy technicke praxe k zastreseni je budova Opery v Pekingu. V tomto pripade bylo k zastreseni pouzito:
1. kulove plochy H=2
2. plochy elipsoidu H=4
3. valcove plochy H=6
4. plochy kruhoveho konoidu H=8
5. plochy anuloidu H=10

Beijing Opera, Peking, Cina
I) Na obrazku je zachycena sportovni arena v Calgary ve state Alberta, Canada. Jeji zastreseni bylo realizovano pomoci plochy:
1. jednodilneho hyperboloidu I=-2
2. primeho parabolickeho konoidu I=-1
3. hyperbolickeho paraboloidu I=0
4. Pluckerova konoidu I=1
5. Stramberske truby I=2

sportovni arena v Calgary
J) Za jednu z vubec prvnich ucebnic perspektivy je povazovana kniha Di prospectiva pingendi z roku 1480. Jejim autorem je:
1. Tommaso di Ser Giova Mone Cassai - Masaccio J=2
2. Paolo di Dono - Uccello J=3
3. Donato di Niccolo di Betto Bardi - Donatello J=5
4. Leone Battista Alberti J=7
5. Piero della Francesca J=11
6. Fra Filippo Lippi J=13

portret autora
K) Jiz predrenesancni umelci si casto pomahali ruznymi metodami, ktere jim usnadnovaly praci. Ucinnym prostredkem byla ctvercova sit v pudorysne rovine (tzv. pavimentum - dlazba) a jeji perspektivni obraz. Leone Battista Alberti v roce 1435 napsal dilo O malirstvi (Della Pittura libri tre). V tomto dile mimo jine popisuje i nekolik zpusobu zobrazeni pavimenta. Konstrukce na obrazku se nazyva:
1. Costruzione legittima K=1
2. Florentska metoda konstrukce pavimenta K=2
3. Costruzione albertina K=3
4. Holbeinova konstrukce pavimenta K=5
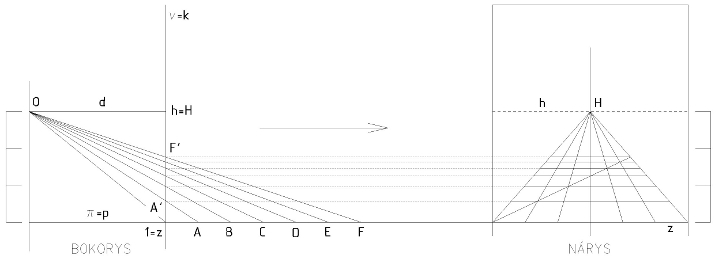
Konstrukce pavimenta
L) Autorem nize uvedene svetozname a naprosto dokonale perspektivni skici je:
1. Carlo Crivelli L=1
2. Raffaelo Santi - Rafael L=3
3. Albrecht Durer L=6
4. Leonardo da Vinci L=10
5. Michelangelo di Lodovito Buonarroti Simoni L=15
6. Tiziano Vecellio L=21

skica
M) Za zakladatele novodobe deskriptivni geometrie je povazovan Gaspard Monge. Zacal jako prednasejici na vojenske akademii v Meziees (1768 - 1789), z jeho prednasek o stavbe pevnosti rozvinul jako zvlastni odvetvi geometrie - deskriptivni geometrii. Za rok vzniku deskriptivni geometrie je povazovan letopocet, kdy vyslo jeho stezejni dilo Geometrie Descriptive. Bylo to roku:
1. 1812 M=1
2. 1790 M=7
3. 1799 M=19
4. 1789 M=37
5. 1766 M=61
Pozn. Nektere prameny uvadeji rok vydani o rok drive, nez je zde uvazovana odpoved.

Gaspard Monge
Finalni souradnice :
N 49° 12.X1X2X3 E 016° 35.Y1Y2Y3
kde:
X1=C-B
X2=J-L+K
X3=(G+I+D+A)/H
Y1=(D+M)/(A+E)
Y2=H+F
Y3=J-F-K

Vzhledem k pomerne velkemu vyskytu mudlu v oblasti finalnich souradnic behem pracovnich dnu, planujte odlov na brzke ranni hodiny, pozdni vecerni hodiny nebo vikendy. Obzvlast v budove naproti je pres den mooc oci, Tak at kes vydrzi
Samotna keska je takova mensi micro, tak setrete misto :-). V kesi neni tuzka!
 
|