Slovensko:
Ta zaklad je del serije puzzle geo-zakladov:
- Crypto I: Ancient
- Crypto II: Cipher
- Crypto III: Key
Ti trije zakladi vam bodo pokazali svet kodiranja podatkov, ki z informacijsko tehnologijo vedno bolj vdira v vsakodnevno življenje. Ce vas bo tema zanimala bolj lahko vec preberete tukaj. Zakladi somed seboj neodvisni, vendar je priporocljiv gornji vrstni red.
Pred reševanjem tega geo-zakalda je potrebno prebrati opis za Crypto II: Cipher, saj je v tej uganki uporabljen isti nacin kodiranja, dekodiranja in ista tabela znakov. Priporocljivo, vendar ne nujno, je tudi, da ga rešite preden se lotite te uganke.
Kot ste videli, je edina 'skrivnost', ki je potebna pri kodiranju, kodirni kljuc. Ta mora biti vnaprej dogovorjen med naslovnikom in pošiljateljem sporocila. Kako se to dogovori brez, da prisluškovalec izve za kodirni kljuc? Vaš sogovornik vam lahko pošlje kovcek v katerem je zakljenjen na listu papirja napisan kodirni kljuc:

Ce je kovcek prispel do vas nepoškodovan, na nepoškodovani roki, lahko predpostavite, da skrivni kljuc ni bil izdan. Lahko si predstavljate, da bi bil tak nacin dandanes dokaj neroden. Vsakic ko bi hoteli pogledati kakšno zakodirano spletno stran (spletna trgovina, spletna banka, ...) bi morali poslati nekoga po en kovcek :). Temu se lahko izognemo z algoritmi za izmenjavo kljuca. Ti omogocijo, da pošiljatelj in prejemnik iz izmenjanih informacij izracunata isti kodirni kljuc. Kljub temu pa možen prisluškovalec nima dovolj informacij, da bi ga izracunal sam. Takšnih algoritmov je kar nekaj, vendar bo tukaj uporabljen
Diffie-Hellman postopek.
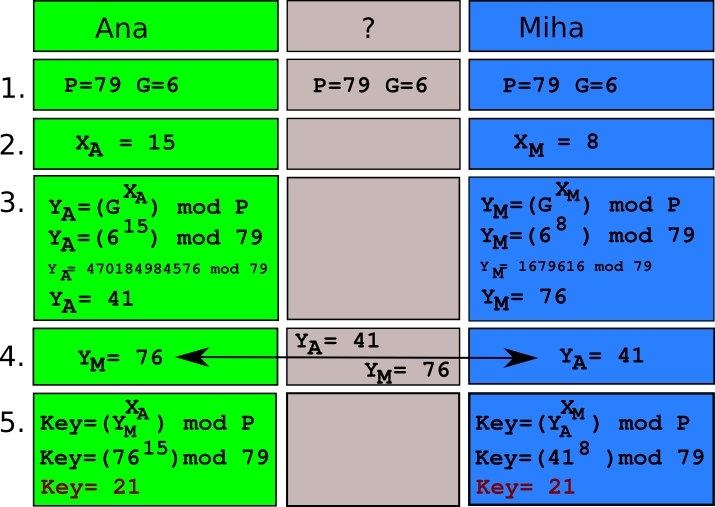
Postopek ima 5 dokaj preprostih korakov in je prikazan na spodnji sliki. Za kljuc se dogovarjata Ana in Miha. Zelena polja vsebujejo informacije, ki jih pozna Ana, modra polja informacije, ki jih pozna Miha, ter siva polja kjer so informacije, ki jih je sposoben slišat vsak prisluškovalec.
Figure 1
|
Koraki so:
- Ana in Miha se dogovorita za dve osnovni števili P in G. Ta števila sliši tudi vsak prisluškovalec. V našem primeru bodo vedno P=79 in G=6.
- Ana si iznisli nakljucno stevilo XA manjše od P. Tudi Miha si izmisli nakljucno stevilo XM manjše od P. Obe izmed teh števil sta skrivnosti, ki jih Ana in Miha obdržita zase.
- Ana izracuna YA=GXA mod P. Operacija (q=x mod y) pomeni, da je q celoštevilcni ostanek pri deljenju x z y. Torej 5 mod 2 = 1. Prav tako Miha izracuna YM=GXM mod P.
- Ana in Miha si izmenjata YA in YM, torej ta števila izve tudi prisluškovalec. Ti dve števili imenujemo Diffie-Hellmanovi števili.
- Ana izracuna kljuc Key=YMXA mod P. Enak rezultat dobi tudi Miha z svojim izracunom Key=YAXM mod P.
Morebiten prisluškovalec tako sliši
P,
G,
YA ter
YM. To ne zadošca, da bi lahko izracunal kljuc za katerega sta se pravkar dogovorila Ana in Miha. Sedaj, ko oba poznata kodirni kljuc lahko z njim zakodirata vso komunikacijo med njima.
Za rešitev te uganke je potrebno razumeti ta postopek in kodiranje opisano pri Crypto II: Cipher. Kot ste morda že opazili iz primera so zaradi potenc lahko števila, tudi v našem preprostem primeru, izjemno visoka. Ker je lahko to prevec za marsikateri kalkulator, lahko potrebni operaciji (potence in mod) racunate tukaj.
Uganka: Skrivnostni lastnik geo-zaklada je dokaj izbircen clovek, in želi da njegov zaklad najdejo le izbranici. Tem je bilo baje zaupano skrivnostno geslo, s katerim lahko pri lastniku dobijo koordinate zaklada. Ker si lastnik hoce zagotoviti anonimnost je poskrbel za komunikacijo preko spleta. Za koordinate zaklada se lahko
pogovorite z njim. Na sreco se je odkril tudi eden izmed geolovcev, ki pozna geslo. Z njim se lahko
pogovorite tukaj. Vam ju uspe pretentati in izvedeti koordinate?
English:
This cache is a part of puzzle geocache series:
- Crypto I: Ancient
- Crypto II: Cipher
- Crypto III: Key
These three caches will lead you into the world of cryptography that more and more becomes a part of everyday life. If you want to know more about the topic you can read here. The caches are independent, however the above order is recommended.
Solving this puzzle geocache will require you to also read the description for Crypto II: Cipher because the same encryption/decryption method will be used here along with the same encoding table. It is recommended, but not necessary, to solve it before this puzzle.
As you learned the encryption key is the only 'secret' needed in encryption. It must be agreed upon between sender and recipient of the message. How do both agree on the encryption key without anyone else knowing it? Your co-responder could send you a locked briefcase containing a piece of paper with the key written on it. If you receive unbroken briefcase on unbroken hand, the key has not been compromised. One can imagine that such a way would be highly impractical in everyday life. Each time you wanted to view an encrypted web page (web-store, web-bank, ….) you would need to send someone out for a briefcase :). This can be avoided with key exchange algorithms. With these two persons can agree upon a key without giving a possible eavesdropper enough information to deduce the key himself. There are many such algorithms, but here a Diffie-Hellman key exchange will be used.
The procedure has 5 simple steps that are shown in figure 1. Ana and Miha are agreeing on the key. Green field represent the info that Ana knows, the blue fields represents that Miha knows, and grey fields are info that possible eavesdropper knows. The steps are:
- Ana and Miha agree in two numbers P in G. These numbers are public and eavesdropper can hear them. In our case we will always use P=79 and G=6.
- Ana chooses a random number XA smaller tha P. Miha also chooses a random number XM smaller than P. Both numbers are a secret and Ana and Marko keep them for themselves.
- Ana calculates YA=GXA mod P. Operation z=x mod y means, that z equals the leftover when dividing x with y, e.g. 5 mod 2 = 1. Miha also calculates YM=GXM mod P.
- Ana and Miha exchange YA andYM, so this numbers are overheard by the eavesdropper . This numbers are called Diffie-Hellman numbers.
- Ana calculates the key Key=YMXA mod P. Equal result is obtained by Miha with Key=YAXM mod P.
Possible eavesdropper therefore knows P, G, YA, and YM. This however does not suffice to calculate the encryption key, that Ana and Miha agreed upon. Now that both Ana and Miha know the key, all communication between them can be encrypted and kept safe from unwanted ears.
To solve this puzzle one must understand the above described procedure and encoding/decoding method described in Crypto II: Cipher. As you might have noticed, the number can get huge because of the exponent, even in out simple case. Sometimes they are too great for ordinary calculators, so you can calculate everything with this one.
Puzzle: Mysterious geocache owner is rather picky person and only wants selected people to find his cache. This people were entrusted with a password which persuades the owner to give them the coordinates of the cache. To ensure the anonymity he devised web pages for communication. You can
talk to him. You can also
talk to one of the geocachers that knows the password. Can you fool them and get the coordinates?