I have been asked to outline a few Intermediate Strategies for Sudoku. Before I continue the advanced series, I've decided to do just that.
There are two main intermediate strategies for solving Sudoku, Triples and Ghost Numbers. By using those two strategies alone (along with the basic ones), you can solve any puzzle in the newspaper except for possibly a few of the Saturday ones. (Well, you can solve the ones that are solvable, but that's a different s rant.) Here I address Ghost Numbers.
As we did with the Triples, let's start very, very basic. Note this diagram. With the 7-8-9 in the blue cells, it is pretty obvious that the cells with the blue Xs CANNOT contain a 7, an 8, or a 9.

Let’s look at this same situation from another point of view. Here the blue cells are empty, but they obviously must contain 7-8-9, although we do not know precisely what goes where. It is not as obvious as the previous example, but it is exactly the same situation. Since the blue cells must contain 7-8-9, the cells with the blue Xs CANNOT contain a 7, an 8, or a 9.

That's all there is to Ghost Numbers--in theory. In practice the Ghosts are far more elusive. Note this diagram. It is similar to the previous one, except that the square has only four cells filled in rather than six. Note the 9 lurking in the lower right square. Its placement ensures that a 9 cannot appear in the bottom three cells of the lower left square. Therefore, the 9 in that square must appear in one of the two blue cells. This is the same situation as the two previous examples. Since the 9 must appear in one of the two blue cells, it CANNOT appear in any of the cells with the blue Xs. In this example, the 9 in the lower left square is a Ghost Number. It doesn’t appear anywhere in the square, but we can still use it to make deductions and eliminations elsewhere in the Sudoku. (Some texts say that the 9 is "Locked" to the blue cells and therefore unable to be anywhere else in the column. If that description makes more sense than a "Ghost Number," feel free to use it instead.)

Here's another variation of this same position. Now we only have two cells completed in the lower left square. Yet we can still make the same deductions. The 9 in the upper left square combined with the one in the bottom row force (lock) the 9 to appear in one of the two blue cells. Therefore, the 9 CANNOT appear in the cells with the blue Xs. However, in this position, we also can make another deduction. The 9 in the left middle 3 x 3 square must appear in one of the yellow cells. This is an awful lot of information that can be deduced from just four digits placed on the Sudoku grid.

Here's another position. The 7 cannot appear in the blue cell so it has to be one of the yellow cells. Therefore the cells with the blue Xs CANNOT contain a 7.

Now, let's get a little fancier. The 9s in the following diagram are again forced to be in (or locked into) the blue cells. We don't know whether they are in the dark blue or light blue cells, but we do know that they can only appear here. Therefore, the cells with the blue Xs CANNOT contain a 9. Some commentators call this position a "Mini X-Wing" based on its similarity to a real X-Wing. If you can wrap your head around this position, it may help you better visualize X-Wings.

When I discussed Triples, I pointed out that different people could look at the same Sudoku from different perspectives. This phenomenon is significant when dealing with Ghost Numbers. Look at the first diagram again. Do you see blue squares placed on a black/white grid? Or do you see a grid with three blue holes? (In the Pattern Recognition biz, they call this the Figure-Ground dichotomy.) Here is the previous example looked at from a different point of view.

Notice that the two 9s prevent a 9 from appearing in the two cells with a blue X. Since there has to be 9 in that column, they must appear in one of the yellow cells. Note that either analysis yields the same result. One point of view shows you that the 9 cannot appear in the six outer cells of the middle square (and therefore must appear in the middle). The other shows you that the 9 must appear in the middle cells (and therefore not in the outer cells). I can’t tell you which perspective is “correct” since they are both equivalent. You have to find what is comfortable for you.
Ghost Numbers are fun. It's kind of like eating potato chips. Once I get started, I can’t stop. Here’s a very common position. Note that the position of the 9 in the bottom row limits (forces, locks) the 9 to be in one of the blue cells. By now, you should be able to tell immediately that the cells with the blue Xs CANNOT contain a 9.

Let's have even more fun and add an 8 to the top row. Concentrate on the center square. We now have yet another "How do you view it" paradox. You may start filling in pencil marks and realize you have a Triple on 5-6-7 in the center column. Or you may look at the whole pattern and "see" 8 and 9 as Ghost Numbers forcing (limiting, locking) themselves to the blue cells. Which do you see first? The 5-6-7 Triple? Or the 8-9 Double resulting from Ghost Numbers? It doesn’t matter. All roads lead to Rome in a Sudoku (to mix a metaphor).

Heck, I'll throw in a bonus: The position of the 1-2-3-4 in the center square means that they CANNOT be in the center three cells of the center column. There are only four other open cells in this column, and these digits MUST reside in those open cells. Hence the yellow cells must contain the 1-2-3-4 from middle column. Different analysis. Same result. You're allowed to do Sudoku however you please--as long as you don't use an automatic solving program, of course. (But I digress...)
Here are the ingredients for recognizing Ghost Numbers:
1. A single digit must be restricted to two or three cells
2. All of these cells are both in a single row and a single box OR a single column and a single box.
3. This arrangement allows you to remove that digits from the other empty cells in that box and/or that row or column.
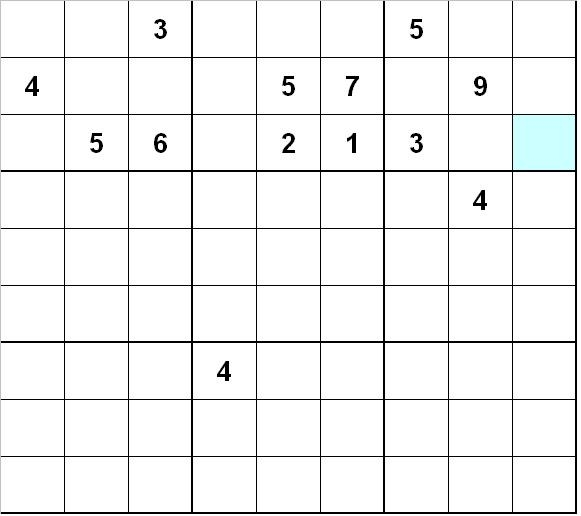
Of course, you didn’t come here just for a Sudoku lesson. You came for a puzzle cache. Here are the puzzles. The first Sudoku will yield X and Y. The second Sudoku will yield Z.
The cache is at N37 32.ABC, W122 17.DEF where:
A = Y
B = X
C = Z
D = X
E = X + Y
F = 2 * Z
If the calculations for E and F result in a two-digit number, take the final digit.
Here is the first puzzle. All single ghost numbers appear in either a row or a column along with a box. In my initial example above, the 7-8-9 ghosts are in a column as are the 9s in the next two examples. The 7 in the next example is a row. The 9 and the 8-9 in the final examples are also in rows. The 1-2-3-4 are in a column and so forth.
This puzzle will yield two different ghost numbers. One is in a row; the other is in a column. The one in the row is X. The one in the column is Y. (For the brute-forcers out there: Yes, X and Y are two DIFFERENT digits and neither is 0.)

Here is the second puzzle. This Sudoku will yield Z. There is only one ghost number. I will not tell you whether it is in a row or a column.

As is my custom, there is a dollar coin for the FTF. Please also note that I DO NOT do sprinkler hides. If for some reason you think you should examine a sprinkler, please do not. The cache is not there.
(This section is not necessary to understand the Ghost Number Technique nor is it part of the puzzle. In fact, it may confuse people who otherwise understood the explanation above. This is a supplemental section that looks at Ghost Numbers from another point of view.)
This cache has been very instructive--for me! Based on some of the comments below and on some private correspondence, I have realized that several people have a lot of difficulty recognizing this technique. The issue is not that they don't understand the concept; the issue is that they look at the ghosts and see them there without realizing it. Two types of puzzlers appear to fall into this category: 1) The Experienced Sudoku Master who has used this technique for so long that it has become second nature, or 2) The Intuitive Puzzler who sees patterns immediately without breaking them down into their components. Normally, this is not an issue since these people blithely go about solving the Sudoku without getting caught up where others might stumble. However, I do realize that these people aren't here to solve Sudoku; they are here to grab a puzzle cache, and I have to make it grabbable for them. Here I attempt a different explanation that may (or may not) help.
Basic Sudoku strategies are all about filling in numbers. Once you fill in one number, then you can fill in another, then another and so forth. Most Intermediate strategies and all Advanced ones are less about filling in numbers than they are about rejecting possibilities. If you reject enough possibilities (eight, to be exact), you are left with a single digit which you then fill in. However, you may have to take several passes to reject the numbers that cannot fit. What I call a Ghost Number is a digit that is restricted to a very tight number of cells in such a way that you can THEN remove possibilities elsewhere. If the restriction doesn't allow you to do something else, it's "nice to know" but not very useful. You need to go looking for something else.
Let's go very basic but starting from a different place. Look at the following position, and study the blue cell. It has to contain a 4. Why?

Look at this marked-up diagram. The position of the three 4's on the grid prevent a 4 from being in any of the empty cells covered by the red arrows. That leaves only one empty cell which can contain the 4: the blue one. This technique is called Cross-Hatching and is the first technique that most people learn. It is basic and fundamental to solving Sudoku. Most people will take a fresh puzzle and do the cross-hatching exercise across all rows and columns in order to fill in all the "obvious" cells before looking for anything more creative. There are no Ghost Numbers here.

Now look at the following diagram. It is almost exactly the same as the previous example but with one fundamental difference: there is NO 4 in the upper middle block. The exercise before you is NOT to figure out where to put the 4 in the upper middle block. It is the same as the first example: what number goes into the blue cell?
Now, DO NOT GET AHEAD OF YOURSELF!!!!!!!!!!!!!!!!!!! In the upper right block there are two cells that can possibly contain a 4, if you restrict yourself to looking at the 4's that you can actually see. So which is it? The blue cell or the one two cells above it?
This diagram will give you the answer. The red arrows show you the cross hatching from the 4's that you can see. This information tells you that, although we DON'T know where to put a 4 in the upper middle block, we do know that it has to be in one of the two cells with the red question marks. Note that these two possibilities are both in the same row. Hence even though there is NO 4 in that row, we know that the upper right cell in the far right block cannot contain a 4. Therefore, the blue cell must contain the 4.

A Ghost Number is a number that is not actually on the grid but is known to be in a limited number of positions. Because the Ghost is known to be limited to those few positions, you can use that information to make deductions elsewhere.
If that doesn't do it for you, let me make one last analogy. Look up how they discovered the planet Neptune. They didn't see it or even know that it existed, but something was screwing up the orbit of the planet Uranus. They were able to use that information to predict more or less exactly where to find the new (Ghost) planet. [I realize this isn't a perfect analogy, but it is a similar situation. If this paragraph winds up confusing more people than helping them, I'll probably delete it.)