Puzzle Secrets Revealed - Binary Numbers #01 Mystery Cache
Puzzle Secrets Revealed - Binary Numbers #01
-
Difficulty:
-
-
Terrain:
-
Size: 
(micro)
Please note Use of geocaching.com services is subject to the terms and conditions
in our disclaimer.
The cache is not at the posted coordinates.
This series "Puzzle Secrets Revealed" is designed to help those
that are new to working/solving puzzles on this site. The main
focus of these caches is to show some of the little tricks that are
used to hide or disguise important information such as the
coordinates.
On each cache page we will tell you what needs to be done to
"solve" that puzzle. This is to show how easy it is to get the
coordinates using one or more of these tricks. We will not spoil or
reveal the tricks on any other cache page unless we have the
written permission of that CO. However what we will be doing is
giving you the knowledge on what to look for and a few things to
try. On this web site there are puzzles that will use one or more
tricks. There are also lot that don't use any. What we will be
showing you in this series are things to try first or to try when
you are not sure what else to do.
Since we are not computer techs, the examples and methods shown are
how we do it. There could be an easier and faster way to do the
same thing.
* * * * *
Before we begin, a few words and ideas need to be talked about.
There are many different number and counting systems. The most
common system we use is called "Base 10" or "Decimal notation" or
just "Decimal". It uses the numbers 0,1,2,3,4,5,6,7,8,9. In this
puzzle we are going to talk about "Base 2", more commonly referred
to as "Binary" or "Binary Numbers". It uses only the numbers 0 and
1.
The Binary Numbers system is said by some to be the most basic of
computer languages there is. The number 1 simply means Yes or On
and the number 2 is simply No or Off. If you were to look at the
history and moderen-day usage of the binary system you would
quickly discover that this simple idea is the beginning of a
mountain of information. There are a lot of rules for formatting
and combining number strings that we are not going to get into. For
this puzzle we are going to look at what these 1's and 0's mean and
how to turn them in to numbers that are easier to understand. For
information on how to turn them in to words, look at Puzzle Secrets
Revealed - Binary Numbers #10.
In our everyday counting (Base 10) the number 6245 represents the
value of 6 thousands, 2 hundreds, 4 tens and 5 ones. In Binary it's
very different but at the same time very simple. In Base 10 you can
have multiples of a value, such as having 6 thousands or 5 ones. In
Binary you have either 1 (one) or 0 (zero) of a value. Here are a
couple examples of binary numbers: 10010011, 1101110, 00110011110,
110, 00110001. A binary number can be any length, from a single
digit to as long as you want.
Binary Numbers to Standard Numbers
To convert a Binary number (Base 2) to an everyday number (Base 10)
the process is very easy. Write out a line of Base 10 numbers that
doubles with each step. It starts with 1 then it doubles to 2 then
doubles again to 4, then to 8, 16, 32, 64, 128 and so on. These
numbers are the value for that place. The only thing to remember is
to write it out from the right to the left. So it would look like
this: 128, 64, 32, 16, 8, 4, 2, 1. In a Binary number it is said
that the 1's are turning on the value and the 0's are leaving it
off. So to find out what a binary number is equal to, just add up
all the values that have a 1 in it and disregard the values that
have a 0.
Here is how to decode a binary number with simple pen and
paper.
First get or find the number, in this case we are going to use
0001101001
Next write from right to left; 1 then 2 then 4 and so on until it
looks like this
Then place the binary number you want to decode under it
(0001101001), one digit per space, with the right-most binary
number under the right most digit you wrote out, which is the
1.
Then add together the numbers that have a 1 under them. These are
the values that are turned on. Which, in this example would be
64+32+8+1 and equals 105.
As we stated there are certain rules for writing and formatting
multiple strings of binary numbers. But to keep it simple each
group of numbers will either be separated by a space or on its own
line:
0101111 100011 110000010
1111010
001001
10000111
Most of the time the leading 0's are dropped since they have no
value. 00000101 is the same as 000101 or 00101 or 101. They all
equal 5.
Standard Numbers to Binary Numbers
To change a Base 10 number into a Binary number is also so very
simple. Once again writing right to left, create the number grid,
starting with 1 on the right followed by a 2 then a 4, 8, 16 and so
on until you get to a number that is larger than or equal to the
number you want to write as a Binary number. For example, if the
number you wanted to change over was 179, then the number grid
would look like this:
Then you would find the largest number on the grid that is equal to
or less than the number you are working with and place a 1 right
below it. Since our number is 179, the largest number without going
over is 128. So the grid will now look like this:
The next step is a little tricky because you will be repeating it
over and over, but each time it will be with a smaller number. Take
the number you want to change and then subtract from it the value
you had just put a 1 under. In this case take 179 and subtract 128
from it, which gives you 51. 51 is now your new number that you are
working with. On the grid, start with the value one place to the
right of the number you just placed the first 1 under. In this
example it's 64. As before, we are looking for the largest number
on the grid that is equal to or less than the number you are
working with. Since 64 is larger 51, we don't put a 1 under it, so
we would need to place a 0 there.
Moving one more place to the right, the next value is 32, which is
the largest number without going over 51. So we place a 1 under
this number and once again we do a little math and subtract 32 from
the current number we are working with which is 51. This gives us
19. Keep repeating these steps until the current number you are
working with reaches zero. At this point if there are any Binary
values remaining to the right, place a 0 under them If done
correctly the grid should look like this:
Which is written out like this: 10110011.
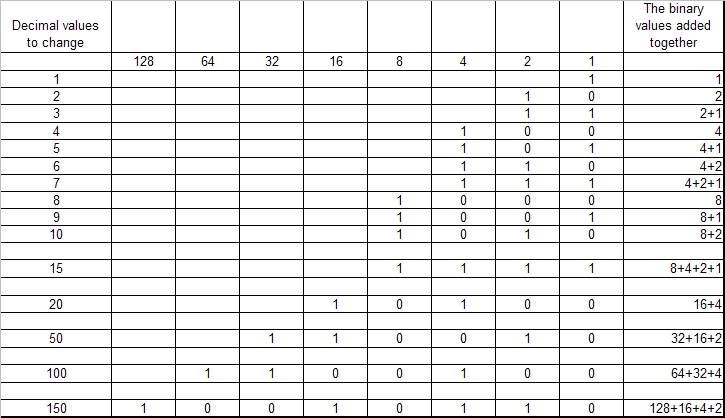
Here is a simple chart to show how this works with a few
numbers.
For advanced puzzles, this simple number system could use "dog and
cats" or "boats and planes" instead of 1's and 0's.
Now a little Binary Number joke we found: There are only 10 types
of people in the world. Those that understand binary and those that
don't.
Joke explained: The binary number 10 is equal to our normal
counting of 2.
And on with the puzzle. I'm going to keep it simple since you have
already done a lot of reading.
AA = 00101111
BB = 00011001
CCC = 11101110
DDD = 1111010
EE = 0001111
FFF = 1001110001
The cache can be found at: North AA BB.CCC West
DDD EE.FFF
Check your solution and get parking coordinates
Even though some will be tempted to do this at night, please don't
due to the patrolling security for nearby businesses. Even though
this is city property, any activity after hours could draw
suspicion.
We are trying something different with the cache container. To open
it, wiggle and pull.
There's a nice $2 bill as the FTF prize.
*** Congratulations to WellJointed on getting the
FTF***
Additional Hints
(Decrypt)
Nobhg guerr srrg sebz znva genvy.