The 10x10 grid below has a descriptive border column and row on the top and left side, respectively. The problem is to black out two nonadjacent squares in each column and row and then write the digits 1 through 8 once each in the eight remaining squares. Each run of adjacent digits must add up to the corresponding sum shown on the left or top. If neither black square is at the start or end of the row or column, there are three runs; if just one is at the end, there are two. If both are at the ends, there would be just one run, but this does not occur in the problem below.
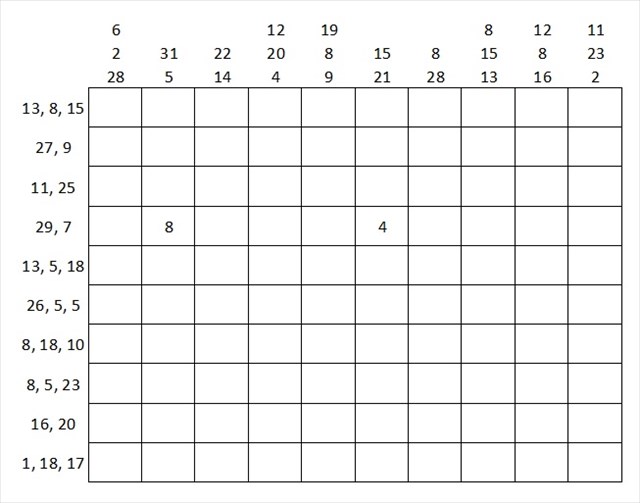
This should be a fun pencil and paper exercise in logic. Once you have solved the grid it's time to test your ability to follow instructions. Use the following instructions to get the coordinates to the cache:
- Locate the first black square in the third row from the top. Look at the eight squares immediately surrounding this black square. Find the number that is repeated. This is A.
- Locate the second black square in row five. Take the number directly to the left and the number directly to the right and add them together. The result is B.
- Locate the second black square in row eight. Take the number directly above it and subtract this from the number directly to the right of the black square. The result is C.
- Locate the first black square in column four. Count the number of black squares immediately surrounding this one. That number is D.
- Locate the first black square in column six. Count how many of the surrounding squares contain numbers. This count is E.
- Find the first black square in column ten. Add the smallest and largest numbers that immediately surround this square. The result is F.
Now fill in the following coordinates:
N 35 49.ABC
W 078 53.DEF
