Nachdem Bert Hill einige Jahre in seinem wunderschön parkettierten Loft gelebt hat (siehe hier) will er sich ein wenig verändern. Nach wie vor ist er begeistert von Parketten und nach wie vor ist er inspiriert von den Arbeiten des berühmten Kieler Mathematikers H. Deshalb beschließt Bert etwas sehr Ungewöhnliches: Er will nicht einen vorhandenen Raum mit Parkett auslegen - nein, er will einen Raum extra so bauen, dass er ein ganz besonderes Parkett umschließt. Und zwar ein Parkett aus solchen Steinen und mit solchen Eigenschaften wie sie der Kieler Mathematiker gefunden hat: 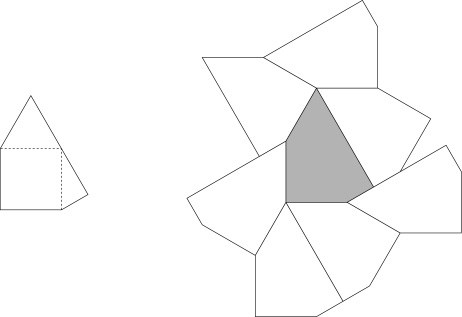
Solch ein Parkett ist nach folgenden Regeln aufgebaut:
- Es besteht aus lauter gleichartigen Teilen
- Die Teile dürfen beim Parkettieren beliebig gedreht und gespiegelt werden, jedoch natürlich nicht zerteilt.
- Ausgehend von einem Teil in der Mitte soll versucht werden weitere Teile so -ohne Lücken und Löcher- um das erste Teil herum zu gruppieren bis es vollständig eingeschlossen ist. Vollständig eingeschlossen ist das Mittelteil erst dann wenn wirklich jede Kante und jede Ecke umschlossen ist. Der Rand darf beliebig ausgefranst sein, aber eben kein "Loch" umschließen.
- Ist es gelungen, eine solche Corona um das erste Teil herum zu legen, so soll nun versucht werden aus weiteren Teilen einen zweiten vollständigen Ring um den ersten Kranz herum zu legen. Natürlich auch wieder ohne Lücken und Löcher und auch wieder so, dass jede Kante und jede Ecke des inneren Bereichs völlig umschlossen ist.
- Und so macht Mann noch einige Male weiter - es gilt einen Parkettstein und ein daraus resultierendes Parkett zu finden, das möglichst viele Coronen aufweist.
- ABER: "möglichst viele" soll nicht bedeuten "unendlich viele". Das heißt: Es soll nicht möglich sein, mit den Parkettsteinen die vollständige Ebene lückenlos zu parkettieren! Anders formuliert: Nach einer gewissen Anzahl Kranzschichten muss Schluss sein - es muss zwangsläufig zu einer Konstellation kommen, bei der es dann nicht mehr möglich ist, noch eine weitere Corona zu bilden!
Wie oben ersichtlich ist es dem Kieler Mathematiker H. prinzipiell gelungen, solch ein Parkett zu konstruieren. Allerdings konstatiert Bert, dass H. bezgl. Punkt 4. und Punkt 5. nicht sonderlich weit gekommen ist. Das Parkett von H. besteht nur aus Mittelstein und einer einzigen Corona. Bert möchte Mittelstein und jede Ringschicht mit einer eigenen Farbe einfärben - und dafür sind ihm zwei Farben einfach zu wenig.
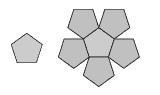 Er macht sich also selbst ans Werk und fertigt einige Skizzen an. Zunächst versucht er es mit einem regelmäßigen Fünfeck, merkt aber schnell, dass er damit keinen einzigen Ring gemäß Regel 3 um das Mittelteil legen kann.
Er macht sich also selbst ans Werk und fertigt einige Skizzen an. Zunächst versucht er es mit einem regelmäßigen Fünfeck, merkt aber schnell, dass er damit keinen einzigen Ring gemäß Regel 3 um das Mittelteil legen kann.
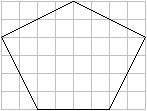 Er konstruiert mühsam ein weiteres fünfeckiges Parkettelement mit günstigeren Winkeln,
Er konstruiert mühsam ein weiteres fünfeckiges Parkettelement mit günstigeren Winkeln,  aber auch diese Idee muss er gleich wieder verwerfen, weil damit leider doch beliebig große Flächen parkettiert werden können und somit Punkt 6. von oben verletzt wäre.
aber auch diese Idee muss er gleich wieder verwerfen, weil damit leider doch beliebig große Flächen parkettiert werden können und somit Punkt 6. von oben verletzt wäre.
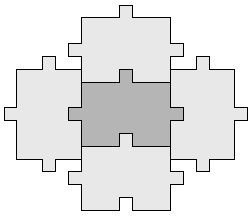 Doch dann kommt Berts Durchbruch: Er findet sein erstes Teil, mit dem er ein Zwei-Farben-Parkett nach den obigen Regeln konstruieren kann. Dieses Teil nennt er "Stein X".
Doch dann kommt Berts Durchbruch: Er findet sein erstes Teil, mit dem er ein Zwei-Farben-Parkett nach den obigen Regeln konstruieren kann. Dieses Teil nennt er "Stein X".
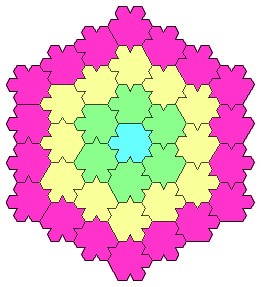 Doch weiter kommt Bert selbst erst mal nicht und er sucht im Internet. Ja, da haben andere tatsächlich schon bessere Parkette gefunden, wie z.B. dieses Vier-Farben-Parkett links.
Doch weiter kommt Bert selbst erst mal nicht und er sucht im Internet. Ja, da haben andere tatsächlich schon bessere Parkette gefunden, wie z.B. dieses Vier-Farben-Parkett links. 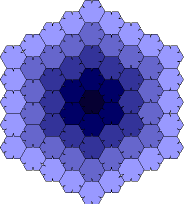 Manche Internet-Quellen behaupten sogar, aus diesen Steinen ließe sich ein Fünf-Farben-Parkett konstruieren, aber dann hätte die vierte Corona Löcher - und das ist gemäß Regel 3 nicht erlaubt (und wäre ja irgendwie auch kein Parkett, oder?)
Manche Internet-Quellen behaupten sogar, aus diesen Steinen ließe sich ein Fünf-Farben-Parkett konstruieren, aber dann hätte die vierte Corona Löcher - und das ist gemäß Regel 3 nicht erlaubt (und wäre ja irgendwie auch kein Parkett, oder?)
Tja, und an dieser Stelle steckt Bert seit Wochen und Monaten. Er hat schon viele Parkettsteine konstruiert, zahlreiche Karopapier- und Wabenmuster-Zettel vollgekritzelt, ausgeschnitten, geklebt, gebastelt...
Hierbei bittet Bert um Mithilfe. Wem gelingt es, ein Sechs-Farben-Parkett zu konstruieren? (Wenn es jemandem gelänge, sogar ein Sieben-oder-noch-mehr-Farben-Parkett zu finden wäre das eine Sensation! Solch ein Parkett ist noch nicht bekannt (aber es ist auch nicht widerlegt, dass es eines geben könnte). Als kleinen Anreiz hat Bert auch einen Schatz versteckt - und zwar hier:
 Gebrauchsanweisung für die Formel: Ihr müsst also eigentlich 24 einzelne Rätsel lösen - und zwar gilt es für jeden Stein A-X herauszufinden, ein wieviel-farbiges Parkett mit ihm gelegt werden kann. Diese Zahl ist dann jeweils für den jeweiligen Buchstaben in die Formel einzusetzen. Und was ist wenn man mit einem oder mehreren der Steine ein unendlich großes Parkett legen könnte? Dann setzt der Einfachheit halber 2 für den jeweiligen Stein in die Formel ein.
Gebrauchsanweisung für die Formel: Ihr müsst also eigentlich 24 einzelne Rätsel lösen - und zwar gilt es für jeden Stein A-X herauszufinden, ein wieviel-farbiges Parkett mit ihm gelegt werden kann. Diese Zahl ist dann jeweils für den jeweiligen Buchstaben in die Formel einzusetzen. Und was ist wenn man mit einem oder mehreren der Steine ein unendlich großes Parkett legen könnte? Dann setzt der Einfachheit halber 2 für den jeweiligen Stein in die Formel ein.
Viel Spaß bei Schatzsuche, Lösungsfindung per Papier und Bleistift und/oder Basteleien! Anbei zur Inspiration und Erleichterung noch Berts bisherige Skizzen und Bastelbögen.
Noch ein paar letzte Anmerkungen: Ja, das Rätsel ist verflixt schwer. Um ein wenig Ausschneiden und Puzzleteilelegen, Kopieren und Skizzieren auf Karo- oder Hex-Papier werdet ihr wohl nicht drum rum kommen. Manche Steine lassen sich per Suchmaschine finden und bestimmen; für die Steine B, D, H, I, N, R, S, U und V bin ich jedoch verantwortlich. Sollte mit dabei ein Fehler unterlaufen sein bitte ich vorab um Entschuldigung. Wer also auf keine sinnvolle Koordinate kommt darf mich gern vorab mit seinen Zwischenergebnissen kontaktieren. Ich bin gespannt!
Möglicherweise sind die Steine in den Skizzen nicht ganz exakt getroffen; hierfür bitte ich um Nachsicht. Es sollte aber stets klar sein, wie es gemeint ist. Es liegt also keine Falle darin, wenn beispielsweise ein Schlüsselzacken um einem Millimeter nicht in den Schlosszacken passt, haltet es dann nach der Devise: Passt schon!