Archaeologists have discovered that knot tying dates back to prehistoric times. Besides their uses such as recording information and tying objects together, knots have interested humans for their aesthetics and spiritual symbolism. Knots appear in various forms of Chinese artwork dating from several centuries BC (see Chinese knotting). The endless knot appears in Tibetan Buddhism, while the Borromean rings have made repeated appearances in different cultures, often representing strength in unity. The Celtic monks who created the Book of Kells lavished entire pages with intricate Celtic knotwork.
A mathematical theory of knots was first developed in 1771 by Alexandre-Théophile Vandermonde who explicitly noted the importance of topological features when discussing the properties of knots related to the geometry of position. Mathematical studies of knots began in the 19th century with Gauss, who defined the linking integral (Silver 2006). In the 1860s, Lord Kelvin's theory that atoms were knots in the aether led toPeter Guthrie Tait's creation of the first knot tables for complete classification. Tait, in 1885, published a table of knots with up to ten crossings, and what came to be known as the Tait conjectures. This record motivated the early knot theorists, but knot theory eventually became part of the emerging subject of topology.
A useful way to visualise and manipulate knots is to project the knot onto a plane. At each crossing, to be able to recreate the original knot, the over-strand must be distinguished from the under-strand. This is often done by creating a break in the strand going underneath. The resulting diagram is an immersed plane curve with the additional data of which strand is over and which is under at each crossing.
Traditionally, knots have been catalogued in terms of crossing number. Knot tables generally include only prime knots, and only one entry for a knot and its mirror image (even if they are different). The number of nontrivial knots of a given crossing number increases rapidly, making tabulation computationally difficult. Tabulation efforts have succeeded in enumerating over 6 billion knots and links. The sequence of the number of prime knots of a given crossing number, up to crossing number 16, is 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705...
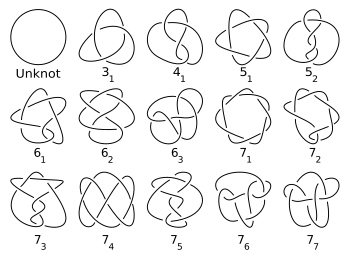
The notation simply organizes knots by their crossing number. One writes the crossing number with a subscript to denote its order amongst all knots with that crossing number. This order is arbitrary and so has no special significance (though in each number of crossings the twist knot comes after the torus knot)
Links are written by the crossing number with a superscript to denote the number of components and a subscript to denote its order within the links with the same number of components and crossings.
Gauss Code, similar to Dowker Notation, represents a knot with a sequence of integers. However, rather than every crossing being represented by two different numbers, crossings are labeled with only one number. When the crossing is an overcrossing, a positive number is listed. At an undercrossing, a negative number.
For example, the trefoil knot in Gauss Code can be given as: 1,−2,3,−1,2,−3
The Gauss code for knot diagrams is perhaps the easiest to describe. Suppose we have a diagram for some oriented knot. Arbitrarily, pick a point P on the knot that is not on a crossing. Then follow the orientation of the knot to arrive at the first crossing, and label it 1. Then, follow the strand to the next crossing. If the crossing you arrive at is not already labeled, then label it 2 (i.e. one greater the crossing you last labeled). Else, skip this crossing and proceed to the next one. Repeat this procedure until all the crossings are labeled (once).
Given this labeling of the crossings, the notation is derived by walking the knot again, starting at P. As we follow the knot, we record the crossings we encounter, keeping in mind that if we happen to traverse a crossing by an under-crossing strand, then we record the label of the crossing with a negative sign. The procedure terminates when you walk the whole knot. For 12 crossing knots a second sign convention is used: if the crossing is right handed it is given a positive sign, otherwise a negative sign.

For the example diagram, the Gauss code will be:
1 -2 3 -4 5 6 -7 -8 4 -9 2 -10 8 11 -6 -1 10 -3 9 -5 -11 7
Take a look at the knots below






Bring your own Pen
