
Na matemática, o número  é uma proporção numérica que tem origem na relação entre o perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro
é uma proporção numérica que tem origem na relação entre o perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro
e diâmetro 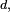 então aquele número é igual a
então aquele número é igual a 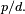 É representado pela letra grega
É representado pela letra grega  .
.
Grandezas que dependem de 
Várias relações matemáticas dependem do conhecimento da constante 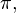 as mais conhecidas a nível didático são:
as mais conhecidas a nível didático são:
- Perímetro de uma circunferência:
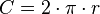
- Área do círculo:
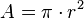
- Volume de uma esfera:

Métodos de cálculo
A primeira tentativa rigorosa de encontrar  deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que
deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que  seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de
seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de  .
.
Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou  tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.
tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.
A busca pelo valor de  chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung Chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.
Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62.000. O resultado é aproximadamente uma circunferência de diâmetro 20.000". O valor de 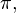 portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de
portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de  . Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.
O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Ghiyath al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de  com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados.
com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados.
Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para 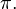
Cronologia do cálculo de 
| Matemático |
Ano |
Casas Decimais |
| Egípcios (Papiro de Rhind) |
1650 A.C. |
1 |
| Arquimedes |
250 A.C. |
3 |
| Zu Chongzhi |
480 D.C. |
7 |
| Ghiyath al-Kashi |
1424 |
16 |
| Ludolph van Ceulen |
1596 |
35 |
| Georg von Vega |
1794 |
126 |
| Gauss |
1824 |
200 |
| William Shanks |
1874 |
527 |
| Levi B. Smith, John W. Wrench |
1949 |
1.120 |
| Daniel Shanks, John W. Wrench |
1961 |
100.265 |
| Jean Guilloud, M. Bouyer |
1973 |
1.000.000 |
| Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura |
1982 |
16.777.206 |
| Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo |
1987 |
134.217.700 |
| Chudnovskys |
1989 |
1.011.196.691 |
| Yasumasa Kanada, Daisuke Takahashi |
1997 |
51.539.600.000 |
| Yasumasa Kanada, Daisuke Takahashi |
1999 |
206.158.430.000 |
| Yasumasa Kanada |
2002 |
1.241.100.000.000 |
| Daisuke Takahashi |
2009 |
2.576.980.370.000 |
| Fabrice Bellard |
2010 |
2.699.999.990.000 |
| Shigeru Kondo & Alexander Yee |
2010/08/02 |
5.000.000.000.000 |
| Shigeru Kondo & Alexander Yee |
2011 |
10.000.000.000.000 |
| The Santa Clara University |
2013 |
8.000.000.000.000.000 |
Enigma
Esta cache mistério faz parte de um conjunto de duas caches gémeas que foram lançadas para comemorar o dia internacional do  a 14 de Março de 2015 pois, em notação americana, a data estreve-se 3.14.15. Apesar da efeméride ser comemorada anualmente utilizando apenas o mês/dia, apenas uma vez por século temos a acorrência da sequencia mês/dia/ano.
a 14 de Março de 2015 pois, em notação americana, a data estreve-se 3.14.15. Apesar da efeméride ser comemorada anualmente utilizando apenas o mês/dia, apenas uma vez por século temos a acorrência da sequencia mês/dia/ano.
GC5NXBC - Mistery of Pi - Mafra
GC5NXBD - Mistery of Pi - Portalegre
Como  e torta (pie) em inglês tem sons semelhantes, é também tradição comer-se uma neste dia ou, em alternativa, qualquer prato de forma redonda como piza ou hamburgeres.
e torta (pie) em inglês tem sons semelhantes, é também tradição comer-se uma neste dia ou, em alternativa, qualquer prato de forma redonda como piza ou hamburgeres.
N A B.C W D E.F
Para resolver este enigma é necessário calcular as casas décimais de  e retirar os valores contidos nas seguintes posições:
e retirar os valores contidos nas seguintes posições:
- A - 43 e 44
- B - 95 e 96
- C - 3556 a 3558
- D - 2806 a 2808
- E - 89 e 90
- F - 590 a 592
Nota: Apenas contam as casas décimais. A casa das unidades e o "." não deverão ser considerados.




