Osterhasenakademie Georg Franck von Franckenau Teil 1
Pflichtfach: Experimentelle und numerische Mathematik - spezielle Eirologie
Aufgabenkomplex: Kombinatorik, theoretische und praktische Prüfung (Taschenrechner sind zur Prüfung zugelassen, Konvention: [N/O])
Was sind die Ei-Linie und das Oval?
Darüber gibt es keine eindeutige Definition. Meistens definiert man eine in sich geschlossene Linie, die die Form eines Hühnereis hat oder ellipsenförmig ist. eine Eikurve oder auch Eilinie ist der Umriss eines Hühnereis. Die bekannte Form des Hühnereis wird an einem Ende schmaler und hat nur eine Symmetrieachse. Die Kurven sind konvex. Sie sind stückweise zweimal stetig differenzierbar und haben eine echt positive Krümmung.
Es wird zwischen dem Oval, der Eifigur und dem Eikörper unterschieden, genauso wie zwischen der Kreislinie, der Kreisfläche und der Kugel unterschieden wird.
Die Ellipse
Die Punkte P, welche eine Entfernung von zwei festen Punkten F1 und F2 eine konstante Summe haben, bilden eine Ellipse. Die Parameter a und b sind die beiden Halbachsen, F1 und F2 die Brennpunkte der Halbachsen. In einem Koordinatensystem hat die Ellipse in der Mittelpunkts Lage die Bestimmungsgleichung 
.
Die Ellipse ist dann der Graph dieser Relation. Für a=3 und b=2 sowie 2a=6 folgt unten stehende Ellipse.
Aus zwei Ellipsen lässt sich die Form eines Hühnereis zusammensetzen.
Die Gärtnerkonstruktion liefert eine Eiform, indem man um drei Punkte, die ein gleichschenkliges Dreieck bilden, nach der Gärtnermethode ein Seil schlingt, das etwas länger als der Umfang (u=a+b+c) des Dreieckes ist. Mit dem gespanntem Seil wird eine geschlossene Linie gezeichnet. Es entstehen Ellipsenbögen, die zusammen ein Ei bilden. Eine Computersimulation verdeutlicht diesen Zusammenhang. Für genaues Arbeiten kommen im Bereich der Scheitelwinkel der Innenwinkel des Dreiecks ABC noch drei weitere Ellipsen hinzu. Das sind Ellipsen um die Seiten AB, AC und BC.
Eine Superellipse entsteht aus der Ellipsengleichung (x/a)2+(y/b)2=1 wenn man die Hochzahl 2 durch 2,5 ersetzt. Damit erhält man: 
Die Betragsstriche stellen sicher, dass die auftretenden Wurzeln definiert sind. Für a=3 und b=2 erhält man eine gleichmäßige Quadrantenfunktion um den Koordinatenursprung. Eine Besonderheit der Superellipse besteht darin, das der dazugehörige Rotationskörper, wenn man ihn aus Holz fertigt, ohne Gewalt auf der Spitze stehen kann (nach Piet Hein). Dies steht zum Kontrast zum berühmten Ei des Kolumbus. Die Superellipse gehört zu den Lamekurven, die folgende Parametergleichung erfüllen: 
Für eine Darstellung einiger Lamekurven setzt man a=3, b=2 und für n die Zahlen. Für den Fall, das der Koordinatenursprung unbekannt oder nicht erreichbar ist, wird ein Kalibrierfaktor (KF=3) eingesetzt.
Von der Ellipse zur Hühnereiform.
Man kann die Hühnereiform aus einem Oval erzeugen, wenn in der Ovalgleichung die Terme abgeändert werden. Dabei wird y oder y2 mit einem Term t(x) multipliziert, so dass bei der Eilinie die y-Werte rechts der y-Achse kleiner und links größer werden und der y-Achsenabschnitt unverändert bleibt. Auf diese Weise wird z.B. die Ellipsengleichung x2/9+y2/4=1 zu x2/9+y2/4*t(x)=1.
Man multiliziert also hier y2 mit t(x).
Beispiele:
Die Ellipsen sind schwarz dargestellt, die farbigen Kurven entsprechen den Termen t(x). Die drei farbigen Eilinien haben in etwa die gleiche gewünschte Form, obwohl die Gleichungen auf den ersten Blick sehr verschieden sind. [720/550] Aber:
t2(x)=1/(1-0,2x) kann als geometrische Reihe geschrieben werden.
Allgemein ist 1/(1-q) = 1+q+q²+..., hier ist 1/(1-0,2x) = 1+0,2x+0,04x²+...
t3(x)=exp(0.2x) kann als Taylorreihe entwickelt werden.
Allgemein ist f(x) = f(0)+x*f'(0)+x²*f''(0)+..., hier ist exp(0.2x) = 1+0,2x+0,02x²+...
Zum Vergleich ist t1(x)=1+0,2*x+0*x²
Die drei Terme t1, t2 und t3 unterscheiden sich in der Reihenentwicklung erst im quadratischen Glied. Man kann leicht ablesen: t1(x) < t3(x) < t2(x) Zeichnet man die drei zugehörigen Eilinien in ein Koordinatensystem, so liegt die rote Eilinie außen, die grüne in der Mitte und die blaue innen. Warum liegt die blaue Eilinie innerhalb der roten?
Zu t2 gehören kleinere vertikale Halbachsen und damit ist die Eilinie flacher.
Ein mechanisch erzeugtes Ei
|
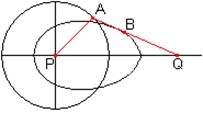
Gegeben sei ein fester Punkt P und ein beweglicher Punkt A, der sich um P mit dem Radius r=PA bewegt. An Punkt A wird eine Strecke a=AQ gehängt, deren freier Endpunkt Q sich auf einer Horizontalen durch P hin und her bewegt. Ein Punkt B auf der Strecke mit BQ=b beschreibt eine Eikurve.
|
|
Eierketten
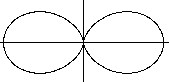Die Polargleichung r(t)=cos²t erzeugt ein Doppelei
(Münger 1894).
Eine zweite Gleichung ist r(t)=exp(cos(2t))*cos²(t)
(Hortsch 1990).
Die Gleichung x4+2x²y²+4y4-x³-6x²-xy²=0 erzeugt ebenfalls ein Doppele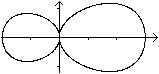
i.
Sinuskurven kann man so verändern und kombinieren, dass man eine Kette von Eiern erhält.
Auch aus Polynomen lassen sich Ketten erzeugen .
Eleganter ist die Darstellung einer Kette durch y² = abs[sin(x)+0,1sin(2x)]:
Weiterführende Literatur zum Studium, Referenzen, Bildnachweise
Weitere Erläuterungen und Ergänzungen findet ihr bei http://www.mathematische-basteleien.de/eilinien.htm. (Bilder und Textteile)
[Lit] www.museo.unimo.it/theatrum/macchine/, Jan Wassenaar
(1) Lockwood, E. H.: A Book of Curves.
Cambridge, England: Cambridge University Press, p. 157, 1967.
(2) Martin Gardner: The Last Recreations, Hydras, Eggs, and Other Math.Mystifications, Springer, New York 1997
(3) Sz.-Nagy, Gyula: Tschirnhaussche Eiflaechen und Eikurven. Acta Math. Acad. Sci. Hung. 1, 36-45 (1950). Zbl 040.38402
(4) Ulrich/Hoffman: Differential- und Integralrechnung zum Selbstunterricht, Hollfeld 1975
(5) Martin Gardner: Mathematischer Karneval, Frankfurt/M, Berlin 1977
(6) Gellert...: Kleine Enzyklopädie - Mathematik, Leipzig 1986
(7) Wolfgang Hortsch: Alte und neue Eiformeln in der Geschichte der Mathematik, München, Selbstverlag 1990, 30S
(8) Gebel und Seifert: Das Ei einmal anders betrachtet, Junge Wissenschaft 7 (1992)
(9) Hans Schupp, Heinz Dabrock: Höhere Kurven, BI Wissenschaftsverlag 1995
(10) Martin Gardner: Geometrie mit Taxis, die Koepfe der Hydra und andere mathematische Spielereien, Basel 1997, Deutsche Ausgabe von (2)
(11) G.F.v.Franckenau: De Ovis Paschalibus. Von Oster-Eyern (= Satyrae medicae, Continuatio 18, Heidelberg 1682, [570/760]
(12) Elemente der Mathematik 3 (1948)
(13) Karl Mocnik: Ellipse, Ei-Kurve und Apollonius-Kreis, Praxis der Mathematik. (1998) v. 40(4) p. 165-167
(14)W. A. Granville: Elements of the differential and integral calculus, Boston, (1929)
(15) Heinz Haber (Hrsg.): Mathematisches Kabinett, München 1983 (ISBN 3-423-10121-0)
------------------------------------------------------------------------------------------------------------------------------------
Nachdem ihr den theoretischen Teil aufmerksam durchgearbeitet habt (es könnte hilfreich sein, einzelne Passagen dabei zu haben), geht es nun zum praktischen Teil. Wo ihr beginnt ist euch überlassen, Haken schlagen gehört ja zur Grundausbildung, es geht natürlich auch in logischer Reihenfolge. Ihr benötigt festes Schuhwerk und angepasste Bekleidung, da es jahreszeitlich bedingt auch mal mehr oder weniger Bewuchs geben kann. Überlegt vorher, wie ihr euren Weg wählt, der direkte muss nicht immer der einfachste sein! Ihr findet an einer Station gleich mehrere Hinweise, dass der OH seine Werkzeuge nicht nur bei der HO oder im Malerfachhandel bezieht. Von diesem Werkzeug bildet einfach die Buchstabensumme und setzt sie als X. Alles Weitere ergibt sich unterwegs.