Dies ist ein Mystery mit einer konkreten Aufgabenstellung.
Man muss nicht unter Einfluss psychedelischer Drogen durch stundenlanges
meditatives Auf-das-Listing-starren erleuchtet werden,
um folgende Frage zu beantworten: "Was ist die Aufgabe?"
Man kann sofort zum zweiten Schritt gehen und die gestellte Aufgabe einfach lösen.
Die oben angegebenen Koordinaten stimmen nicht.
Möchte man aus drei Quadraten Figuren legen,
die an mindestens einer Kante zusammenhängen,
entstehen diese zwei Figuren:
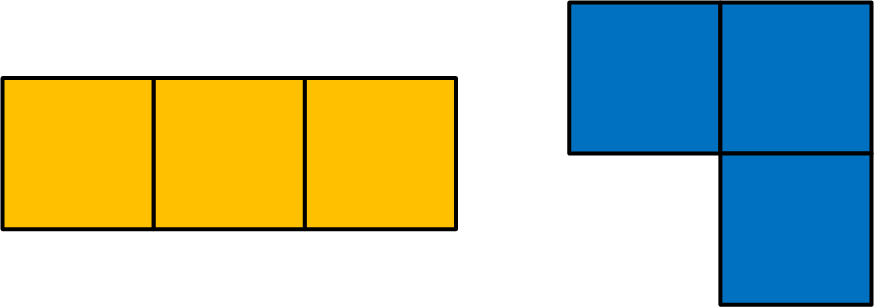
Diese Figuren können natürlich gedreht und gespiegelt werden.
Dann entstehen quasi sechs verschiedene Figuren.
Hier zum Ausmalen, Ausschneiden und Ausprobieren:
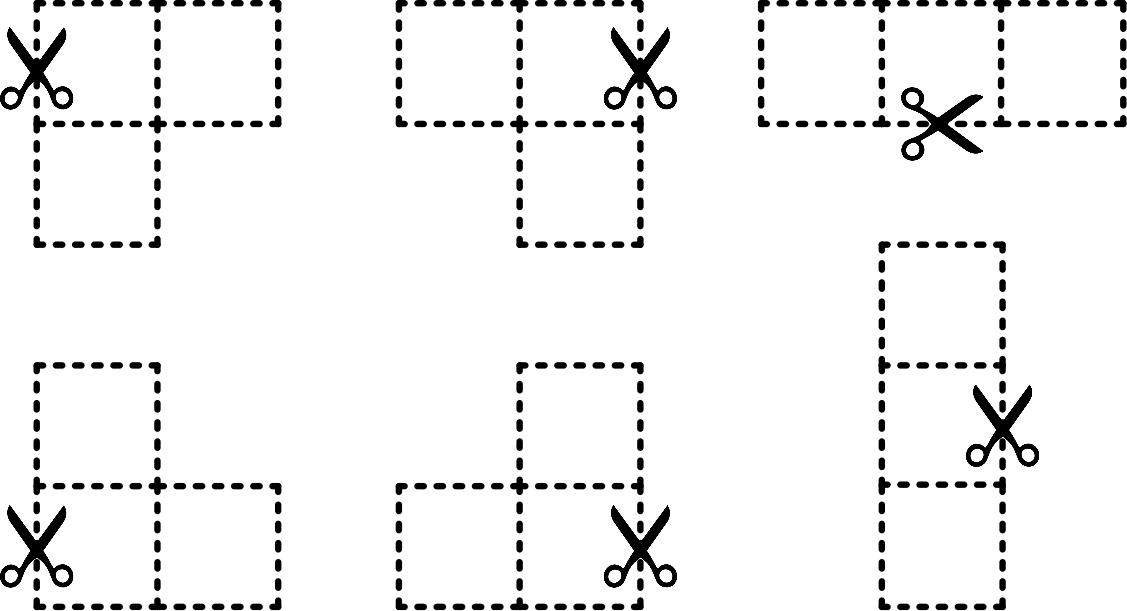
Das Bild kann beliebig oft ausgedruckt und ausgemalt werden.
Begrenzt ist die Anzahl durch deinen Drucker, deinen Papiervorrat
und deine Buntstifte.
Eine Matrix mit m Zeilen und n Spalten,
wobei m oder n durch drei teilbar ist,
kann vollständig mit den oben dargestellten
Figuren ausgefüllt werden.
Hier ein Beispiel:
Bei einer 3x3-Matrix

gibt es 10 Möglichkeiten die
Matrix mit den oben genannten
Figuren zu befüllen:










Noch ein Beispiel:
Bei einer 3x4-Matrix

gibt es 23 Möglichkeiten die
Matrix mit den oben genannten
Figuren zu befüllen:






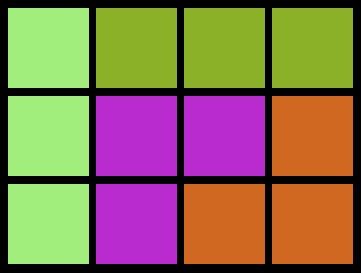
















Und noch ein Beispiel:
Bei einer 3x5-Matrix

gibt es 62 Möglichkeiten die
Matrix mit den oben genannten
Figuren zu befüllen.
Da hier nicht so viel Platz ist,
diesmal als animierte Grafik:

Jetzt endlich zur Aufgabe:
Wieviele Möglichkeiten gibt es eine 12x13-Matrix zu befüllen?

Ordne den einzelnen Stellen deines Ergebnisses Buchstaben zu. Die Einer-Stelle bekommt ein "A", die Zehner-Stelle bekommt ein "B", die Hunderter-Stelle bekommt ein "C", usw.
Anschließend ersetzt du die Buchstaben in den Koordinaten nach dieser Vorschrift mit den Ziffern des Ergebnisses: N 51° 5(A+Y) .UIL E 12° 4J.BGE
Beispiel zur Ermittlung der Werte der Buchstaben:
berechnetes Ergebnis: 415389
| ... |
4 |
1 |
5 |
3 |
8 |
9 |
| ... |
F |
E |
D |
C |
B |
A |
Daraus folgt dann:
A = 9
B = 8
C = 3
D = 5
E = 1
F = 4
...