2^½ eepiifii Mystery Cache

Sohvamysteeri irrationaalilukujen desimaaleihin ja vähän muuhunkin. Tähän mysteeriin saa kaikki tiedot sekä myös vihjettä apuvälineestä kuvauksesta tai sitten chekkeristä, jos osut kuumiin pisteisiin (3 kpl).

Usein kuulee, että joku ei tykkää matikassa ”selitystehtävistä” tai ”sanallisista tehtävistä”. Nyt olisi sellaista mysteerin muodossa tarjolla. Tämän ratkaiseminen ei edellytä mitään korkeatasoista matematiikan loppututkintoa. Hiukan laskimen tms käytön osaamista, yhteen - ja vähennyslaskua sekä tietenkin jotain apuvälineen räpläämistä. Aloituspisteeltä ja kuumista pisteistä ei maastosta löydy mitään tähän mysteeriin kuuluvaa - ovat kartalta katsottuna oivia kätkön paikkoja. Kuumien pisteen osumasta saa aina vihjettä tuonnemmaksi.

Laskimista löytyy näppäimet neliöjuurelle, π (piille) ja joskus myös e:lle. Jos ei löydy e:lle suoraan, niin sitten se löytyy e^x näppäimen kautta (x=1). Φ (Fiille) ei taida löytyä? Sen arvon voi laskea kuvan mukaisesta kaavasta:

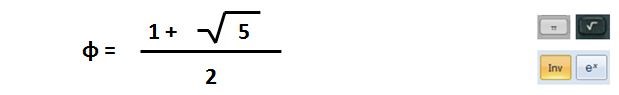
Tulos on 1,ABCDEFGHIJ kymmenen desimaalin tarkkuudella pyöristettynä, pidä se laskimessasi tallessa tarkkana arvona, näytöllä on usein maksimissaan "vain" kymmenen desimaalia! Voit tarkastaa tuloksesi chekkeristä (kuumapiste 1) N60^oEC,ABD JA E25^oFG,HIJ. Sieltä saa myös palan vihjeestä.

Nyt pitäisi vielä olla laskimen näytöllä tarkka arvo Φ ja lopuille se löytyy siis laskimesta yleensä näppäilemällä. Tee laskutoimitus tarkoilla arvoilla: [Neliöjuuri kaksi kertaa ee kertaa pii kertaa fii].

Edellisen kaavan tulon desimaalit ovat KLMNOPQRST kymmenen desimaalin tarkkuudella pyöristettynä. Voit tarkastaa oman ratkaisusi chekkeristä (kuumapiste 2) N60^oKL,MNO ja E25^oQP,RST. Osumasta kuumaan pisteeseen irtoaa taas pala vihjettä.

Unohdetaan molemmista laskutoimituksista muut paitsi 10 ensimmäistä desimaalia ja vähennetään luvusta ABCDEFGHIJ luku KLMNOPQRST ja tulos on yhdeksännumeroinen luku UVWXYZÅÄÖ. Voit tarkastaa tuloksesi chekkeristä (kuumapiste 3.) N60^oYU,VWX ja E25^oÅZ,XÄÖ. Osumasta saa taas vihjeen.

Etsi seuraavaksi, kuinka mones desimaali on kuusinumeroisen lukujonon UVWXYZ ensimmäinen jäsen U π:n (3,14159…) desimaaleista ja se on luku a – kirjoita tulos muistiin. Sitten, kuinka mones desimaali on luvun/lukujonon a ensimmäinen numero e:n (2,71828 …) desimaaleissa ja se on luku b – kirjoita sekin muistiin. Seuraavaksi, kuinka mones desimaali on luvun/lukujonon b ensimmäinen numero neliöjuuri kahden (1,41421…) desimaaleissa ja se on luku c, jonka myös kirjoitat muistiin. Viimeiseksi, kuinka mones desimaali on luvun/lukujonon c ensimmäinen numero Φ:n (1,61803…) desimaaleissa ja tämä on luku d – kirjoita taas luku muistiin. Näissä luku a-d on se järjestysluku, kun kysytty lukujono esiintyy ko. irrationaaliluvun desimaaleissa ensimmäistä kertaa.

Jos edellinen kappale tuntui vaikealta, katso spoilerikuva (Lisätty 8.4.2016).

Laske summat a+b+c = e fgh ijk (Seitsemän numeroinen luku) ja c+d = lmn opq (Kuusi numeroinen luku).

Kätkön löydät, kun ensin löydät koordinaattien minuuttien ja niiden desimaalien muodostamat lukujonot seuraavasti (viisi numeroa):

N60^o_ _,_ _ _ puuttuvat numerot löytyvät π:n gggjf. desimaalista alkaen (tämä+4 seuraavaa numeroa ja on muotoa nn,nnn).

E25^o_ _,_ _ _ puuttuvat numerot löytyvät Φ:n qnqolm. desimaalista alkaen (tämä+4 seuraavaa numeroa ja on muotoa ee,eee).