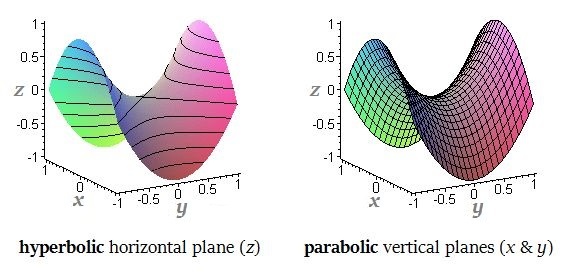
A hyperbolic paraboloid is best defined as an infinite d _ _ _ _ _ - r _ _ _ _ quadric surface having three d _ _ _ _ _ _ _ _ _: one hyperbolic horizontal plane and two parabolic vertical planes, hence the name.
It is represented by the following C _ _ _ _ _ _ _ _ equation:
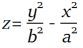
You might notice that one of the parabolas opens d _ _ _ _ _ _ _ while the other one opens u _ _ _ _ _. The degree of c _ _ _ _ _ _ _ _ of the parabolas is determined by the two constants a & b. The hyperbolas (which make up the h _ _ _ _ _ _ _ _ _ cross sections) can open in either the xx- or yy- direction, depending on the chosen value for z. These are important features to note with any hyperbolic paraboloid.
The term "hypar" was introduced by the architect H _ _ _ _ _ _ _ E _ _ _ _ to mean a hyperbolic paraboloid shape, or more formally a p _ _ _ _ _ _ hyperbolic paraboloid, cut from the full infinite surface. The hypar is also often referred to colloquially as a s _ _ _ _ _.
A favourite with mathematicians in the field of geometry, the hyperbolic paraboloid is one of 16 quadric surfaces known to exist in the Euclidean space. More than half of all quadratic surfaces have either hyperbolic or parabolic qualities. Two examples of quadrics which are neither hyperbolic nor parabolic are the c _ _ _ _ _ _ _, and the c _ _ _. There are two kinds of paraboloids: hyperbolic and e _ _ _ _ _ _ _.
The hypar is used in more “every day” practical ways than you might realise: toys (HyPars®), hats, art (origami), bio-engineering, nature (the mantis s _ _ _ _ _), architectural structures (V _ _ _ _ _ _ _ velodrome in London being one of many examples), even food (Pringles).
Its geometry, although seemingly complex, is actually very simple. Spanish-Mexican architect and engineer F _ _ _ _ C _ _ _ _ _ _ built structures that took the hyperbolic paraboloid to new heights (literally). When you think of concrete, you might think of dreary, boxy constructions. Yet this architect was able to use the hyperbolic paraboloid’s thin shell shape and apply it to build huge roof structures. His lightweight, graceful structures may seem delicate, but in fact they’re immensely strong and built to last.
So what makes the hyperbolic paraboloid so strong? It’s essentially how it balances pushes and pulls. All structures must support weight and this weight is ultimately transferred down to the ground. They can do this in two different ways. There’s c _ _ _ _ _ _ _ _ _ _, where the weight squeezes an object by pushing inwards (an arch is an example of a structure that exists in this state). And then there’s t _ _ _ _ _ _, where the weight pulls at the ends of an object, stretching it apart (if you dangle a chain from its ends, every part of it will be in this state). The hyperbolic paraboloid combines the best of both worlds as the concaved (U-shaped) part is stretched while the convex (arch-shaped) part is squeezed. Through double curvature and yet consisting only of straight lines, the shape strikes a delicate balance between these push and pull forces, allowing it to remain t _ _ _ yet surprisingly strong.
The hyperbolic paraboloid - a marvel of mathematical, scientific, ..and culinary genius!

The cache is at S33° 28.???' E151° 20.???'
The way in: There is a very inviting trailhead located on the closest piece of road approx due EAST of GZ. Once you have your coords this explanation should make sense (i.e. there's no real way in from the north or the west and deffo no easy way in from south). Cache and trail are not located on private property.
Please go easy when logging your find on-line so as to not inadvertently (or otherwise!) add any spoilers in terms of the puzzle and the GZ location and please do not post any pics of any part of the actual container or view at GZ. The cache contains a log book and pencil and is large enough for all kinds of SWAG swaps and medium/ large TBs. For FTF we dropped a brand new trackable. We hope you enjoy our first novo mystery cache in this amazing location.