My introduction to Slitherlink happened when I solved a Nelson puzzle cache. Since then I've become somewhat addicted. What better way to spread the addiction than by creating a series of Slitherlink puzzle caches.
The slitherlink rules are easy. You have to come up with a single loop around the grid, in which each numbered square has the specified number of lines around it (for a square grid, the numbers range from 0 to 3). There is only one valid solution.
An interesting aspect of Slitherlink puzzles is that to start with you work at a small scale, looking for patterns of a few neighbouring numbers that let you draw in some initial lines, and to put in some initial crosses (where lines cannot go). As you progress, you have to pay more and more attention to the overall goal of creating a single loop.
Here is a (small) example:

Here is the solution:

Notice that in the solution at each dot either no lines go through it, or two lines meet there. If there was a dot that had one, three or four lines meeting, then we would not have a loop.
This first cache does not involve solving a slither link puzzle. Instead, it is a "boot camp" to prepare you for the puzzles to come. Below are a number of puzzle fragments (one of which is based on a variant that has a non-square grid). In each, you will have to work out how many lines you can fill in, and/or how many crosses you can fill in. [Aside: in an actual puzzle, some of the squares that are blank in the grids below would contain numbers. ]
Here's an example:
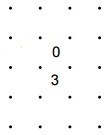
The answer is
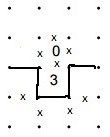
From the information in the example, we have been able to fill in 5 line segments, and also to put in 8 crosses (to mark line segments that are empty in the solution).
Here's another example:

We have a 3 in a corner, and a 1 on the diagonal. The first four scenarios show the four different ways of arranging three lines around a square. The first two are not valid. In both cases we end up with a line that goes into the corner that has nowhere to go, which means there is no possibility of drawing a loop. The next two scenarios are the valid possibilities. Notice that both of them have lines below the 3 and to its left, so we can draw those lines in as part of the solution (which has been done on the fifth scenario). Also notice that (as shown by the arrows) in both valid cases there must be a line leaving the dot to the top right of the 3 that either goes below the 1 or to the left of the 1. That means that the lines above the 1 and to its right must be empty (and we can put crosses there, as shown in the fifth scenario). So, the end result is two lines and two crosses.
To solve the problems below you will have to work through the various possibilities for each square containing a number. A '1' can have 4 different line patterns around it, a '2' can have 6 different patterns, and a '3' can have 4 different pattern. The '1' and '3' situations are mirror images (in the '1' case one of the four side is filled in, whereas in the '3' case one of the four sides is not filled in). Identify the valid patterns for the numbers given. If a particular line segment is present in all valid patterns then fill it in. If a particular line segment must be empty in all valid patterns then put a cross there.
To work out the coordinates of the cache, answer the questions below:
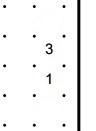 |
A = number of crosses - number of line segments |
Hint: start by considering which patterns around the 3 are valid. |
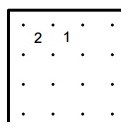 |
B = number of line segments
C = number of crosses |
Hint: start by considering which patterns around the 2 are valid. |
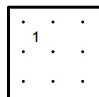 |
H = number of crosses |
|
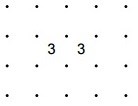 |
E = number of line segments |
Hint: there are 16 arrangements (four for each '3'); which are valid? |
 |
F = number of crosses + 1
G = number of line segments - 1 |
|
 |
D = number of line segments - 1 |
|
The checksum for A to H is 35.
The cache can be found at S 43 3A.BCD E 172 3E.FGH.
The cache is a camo-taped peanut butter jar at the base of a northern post (the western one).
So, get stuck in and train hard for the challenges ahead! To help you in your endeavours, here is some motivational music ...
To further hone your skills, have a go at the following (they are in order of increasing difficulty):
I'm happy to answer questions, give feedback on possible solutions, etc.