Det chiffersystem som heter Playfair skapades av Charles Wheatstone 1854. Playfair är ett lätthanterligt chiffer som ansågs användbart för kortlivad information så sent som under andra världskriget, fast numera kan alla meddelanden knäckas på sekunder med rätt datorpgrogram.
The cipher known as Playfair was created by Charles Wheatstone in 1854. Playfair is an easy to use cipher that was deemed useful for short lived information as late as during World War II. Nowadays any message sent using the Playfair system can be broken in seconds using the correct software.
Svenska
Chiffret
Nyckeln i Playfair är en kvadrat med 25 bokstäver. Eftersom det engelska alfabetet har 26 bokstäver brukar man där antingen byta ut alla j mot i (de ser ungefär likadana ut) eller utesluta q.
En beskrivning av Playfair finns på Wikipedia.
Kvadraten
Normalt sett används ett kodord för att skapa kvadraten och det finns två sätt att skapa kvadraten från kodordet, alla börjar med att man skriver ut kodordet (med dubblerade bokstäver borttagna) följda av de kvarvarande bokstäverna i det 25 tecken långa kodalfabetet. Kodordet i det här exempelt är springtime, och j ersätts med i.
springtmeabcdfhkloquvwxyz
För att skapa kvadraten, fyll i bokstäverna radvis som nedan:
sprin
gtmea
bcdfh
kloqu
vwxyz
Den uppenbara nackdelen med det här är att kodordet står sammanhängande i börjar av kvadraten, och wxyz antingen är i kodordet eller ner till höger. Enligt "The codebreakers, The story of secret writing" av David Kahn så var tanken att skriva ut nyckelordet på en rad och övriga bokstäver på rader under enligt det här schemat:
springtme
abcdfhklo
quvwxyz
Om man sedan fyller i sin kvadrat från kolumnerna kommer kodordet och överblivna bokstäver att spridas ut i kvadraten:
saqpb
urcvi
dwnfx
ghytk
zmleo
Gissningsvis kan förenklingen (som gör chiffret betydligt enklare att knäcka för hand) ha tillkommit när Playfair skulle beskriva Wheatstones chiffer i samband med en middag, och har sedan hängt kvar under de 90 år som chiffret användes.
Givetvis kan man använda en helt slumpad kvadrat också, men då måste nyckeln skapas och förvaras på ett säkert sätt eftersom den inte går att memorera.
En sammanfattning med exempel på hur man krypterar med den här kvadraten: 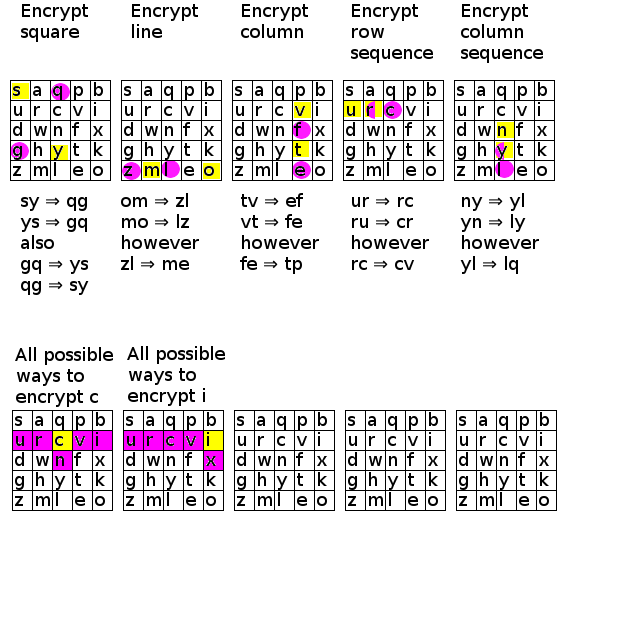
Analys
En viktig sak att tänka på är att playfairkvadraten kan beskrivas som en torus. Det betyder att du kan rotera kvadraten höger-vänster och upp-ner och hela tiden få exakt samma kryptering. Till exempel är bokstaven b i övre högra hörnet ett steg till vänster om s och ett steg under o. Så för att knäcka ett meddelande behöver man inte få fram exakt samma kvadrat, så länge (exempelvis) b är under o och före s.
Läs gärna hela texten på Wikipedia innan du ger dig i kast med den här texten.
Gissa digrafer
Eftersom playfair substituerar digrafer (bokstavspar) så kan man angripa ett kodad meddelande på samma sätt som ett enkelt substitutionschiffer. Skillnaden är att det finns fler digrafer (25x24 = 600 i det här fallet) och att frekvensen är mer jämnt fördelad än för enstaka bokstäver.
Man kan också gissa ord och hitta mönster (re-ce-iv-er till exempel kan krypteras till vm-vl-ui-mv). Ifall motpartern brukar skicka meddelanden på ett standardiserat format (pro forma) kan det vara enkelt att gissa delar av meddelandet, Bletchley Park använde det här för att knäcka många tyska kyptosystem under andra världskriget, inklusive ett Playfair-liknande system. Fyll sedan ut meddelandet efter hand som du får dekrypteringar givna.
Notera också att vi alltid vet att om AB ska bli CD så blir BA DC.
Sammanhängande bokstäver
Titta på hur man krypterar två bokstäver som står intill varandra på rad eller kolumn. Den bokstav som står längst upp i kolumnen eller längst till vänster på en rad kommer att krypteras till den andra. Den andra bokstaven i sin tur krypterar till en tredje bokstav.
Till exempel kan vi se att ru=>cr (även ur=>rc) så vet vi att sekvens urc finns, antingen vågrätt eller lodrätt. Det andra exemplet på bilden är ny=>yl.
När vi har flera sådana här strängar som delar bokstäver kan vi börja sätta ihop dem. Ifall två bokstäver är gemensamma så måste de sitta ihop som en längre sträng (saq och aqp blir saqp).
Ifall mittenbokstaven är gemensam måste de sitter i ett kors (eoz, kob):
k e
eoz eller kob
b z
Ett tredje fall är om en ytterbokstav är gemensam (tkg, gzs), då har vi fyra möjligheter:
tkgzs t tkg t
k z k
g s gzs
z
s
Efter det här steget har vi förhoppningsvis flera bokstavsserier (eventuellt korsande) på tre eller fler tecken samt några avkodade digrafer.
Bokstäver på samma rad
För att "rikta in" sekvenserna tittar vi på vilka kända krypteringar vi har för enskilda bokstäver. Det finns bara fem möjliga krypteringar för varje enskild bokstav, de fyra andra bokstäverna på samma rad eller bokstaven rakt under.
Det här betyder att två bokstäver som kan kryptera till varandra (i exemplet c och i) måste vara på samma rad, för de kan inte båda vara ett steg ovanför varandra.
Det här kan man använda för att hitta om en sekvens är vågrät eller lodrät. Kom ihåg att det maximalt kan vara fem bokstäver i varje rad eller kolumn.
Efter det här steget har vi en eller flera "öar" av kvadraten löst.
klart en av dessa
qpbsa c w
u wnf cny
d y f
Fyll i krypteringar
Nu är det dags att titta på digraferna igen, ifall vi vet var tre av bokstäverna finns kan vi fylla i den fjärde, till exempel om vi fått fram att sn => qd
qpbsa
u
n d
Vilket betyder att de nu finns två möjliga dellösningar:
qpbsa qpbsa
c u w u
nf dw ny dc
y f
Fortsätt på det här viset och utnyttja hela tiden information om vilka bokstäver som kan finnas på respektive rad.
Repetera
Efter det här kan du antagligen helt eller delvis dekryptera fler digrafer vilket ger möjlighet att gissa större delar av meddelandet.
English
The Cipher
The key for a Playfair cipher is a square with 25 letters. Since there are 26 letters in the English alphabet one letter has to be excluded. Usually j is removed and replaced by the similar looking i, or sometimes people omit q. A full description of Playfair can be found on Wikipedia.
The square
Normally a code word is used to create the square, and there are two ways to create a square from the code word. In both cases you start with the code word (after removing duplicate letters) followed by the remaining letters of the 25 characters in the code alphabet. This time, the code word is springtime, and j is repaced by i.
springtmeabcdfhkloquvwxyz
To create the square, fill in the letters row by row like this:
sprin
gtmea
bcdfh
kloqu
vwxyz
The obvious drawback is that the code word is written continously at the start of the square, and that wxyz are either part of the code word or found down to the right. According to "The codebreakers, The story of secret writing" by David Kahn you should instead write the code word on one line and arrange the rest of the letters in the following way:
springtme
abcdfhklo
quvwxyz
If you read the letters out column by column, writing them into the square line by line, you end up with an arrangement where letters from the code word are intermixed with the leftover letters:
saqpb
urcvi
dwnfx
ghytk
zmleo
The simpler way to create the square might have been introduce by Playfair when first describing the cipher system over dinner, and then it stayed that way for the next 90 years that it was in use.
Of course you could use a completely random letter arrangement as well, but in that case you need a way to securely create and distribute code sheets, as the key would be impossible to memorize.
A summary of encrypting using this sample square: 
Analysis
One important observation is that the playfair square is really a torus. This means that you can rotate the square left-right or up-down and always get the same encryption. E.g. the letter b in the top right corner is actually one step to the left of s and one step below o. So you do not have to (and theoretically can't) reconstruct the exact square used in encryption.
Feel free to read the full Wikipedia article before moving on.
Guess digraphs
Since playfair is used to substitute digraphs (pairs of letters) you can attack a coded message in the same way as a simpe substitution cipher. The difference is that there are more digraphs (25x24 = 600 in this case) and that the frequency of digraphs is more equally distributed than for single letters.
It is also possible to guess words and look for digraph patterns (re-ce-iv-er could be encrypted to vm-vl-ui-mv). In case your opponent tend to send standaridized message (pro forma) guessing parts of the message may be trivial, Bletchley Park used this to decrypt many German cipher systems during WW II, including one similiar to Playfair. Keep filling in the message as you find more and more digraph decryptions.
Also notice that for every digraph where AB becomes CD, BA will be DC.
Sequences of letters
Look at how to letters next to eachother (in a row or in a column) are encrypted. The first letter (top of column, leftmost on line) will decrypt into the second letter, which in turn encrypts into a third letter.
From the example you can see that ru=>cr (also ur=>rc) so we know that urc is one sequence, either vertically or horizontally. Another example is ny=>yl.
When we have several of these strings that share one or more letters, we can start piecing them together. If they have two letters in common, they have to form a longer string (saq and aqp becomes saqp).
If they share one letter not at the end of one string, they must form a cross (eoz, kob):
k e
eoz or kob
b z
If they share a single letter at one end of both strings (tkg, gzs), there are four possibilities:
tkgzs t tkg t
k z k
g s gzs
z
s
After this step we should have several letter sequences of three or more letter (possibly even crisscrossing) and some decoded digraphs.
Letters on the same row
To find the correct direction for letter sequences start looking at known encryptions for single letters. There are only five possible encryptions for each single letter, the four letters on the same row and the letter directly below it.
So for two letters to encrypt to eachother (the letters c and i in the image) they have to be on the same row, as they can't both be one step above eachother.
This can be used to find out if a sequence is horizontel or vertical, and thus aligning any connected sequences. Remember that there are only five letters on each line and column.
After this step we should have one or more islands of the square solved.
done one of these
qpbsa c w
u wnf cny
d y f
Fill in encryptions
Now you can look att the digraphs again, if we know where three of the letters in an encryption is, we can fill in the fourth. E.g. if we have seen that sn => qd
qpbsa
u
n d
With n locked in there are now only two possible way to combine what we know:
qpbsa qpbsa
c u w u
nf dw ny dc
y f
Keep doing this, using information about what letters are known to be at a certain line.
Repeat
At this stage you can probably decode more of the digraphs in full or even partially and use this to guess more of the message.
Meddelande / The message
yscså Dusåv vsXxg zpxsj åxvbv åwQpx aQmsk påvvs XxxvA vxQom zånsx Qiwfz xsvxj fAaxc gmxtx vtxxv txaQm skpxf vsvxr vXxåD us
Ok, vad är nu det här?
En blandning av stora och små bokstäver och dessutom ett å. Till råga på allt 26 unika bokstäver i meddelandet (om vi behandlar stora och små bokstäver olika). Fast vi har åtminstone inga bokstavspar som är lika eftersom xx i "gmxtx vtxxv" delas up som "xv-tx-xv".
För att inte göra uppgiften för tidsödande så har jag tre ledtrådar:
- Nyckeln som använts är en kvadrat på 6x6 bokstäver istället för 5x5.
- Texten är på svenska.
- Början på meddelandet är "nordDfemDåtAtaD".
Now what is this?
We have a mixture of upper and lower case letters, and besides that the letter å. On top of this there are 26 uniquee letters in the message (treating upper and lower case letters differently). But at least there are no same-letter digraphs as xx in "gmxtx vtxxv" will be split as "xv-tx-xv".
To make the task less time consuming I will give you three clues:
- The key is a 6x6 square instead of the more common 5x5.
- The text is in Swedish.
- The start of the message is "nordDfemDåtAtaD".
Bonus and checkers
Verify the coordinates for the cache / Kontrollera koordinaterna för cachen:

There is an encrypted bonus message in the cache, remember to make a copy and decrypt it.
Det finns en krypterad bonus i cachen, glöm inte skriva ner och avkoda den.