This cache is hidden for the Taco Tuesday: Pythagorean Theorem Day event. All event attendees who chose to look for and sign the cache are able to claim FTF honors.
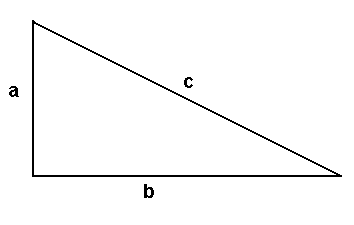
The Pythagorean theorem is a fundamental relation in Euclidean geometry among the three sides in a right triangle. It states that the square of the hypotenuse (c, in the picture above) is equal to the sum of the squares of the other two sides (a and b, in the picture above). The theorem can be written as an equation:
a2 + b2 = c2
The cache is not located at the posted coordinates, but instead at N 42 29.DEF W 083 00.GHJ.
Problem #1: The distance between bases in Major League Baseball is 90 feet. The runner on first base attempts to steal second base. Assuming the catcher releases the baseball DIRECTLY over home plate and the shortstop catches the baseball DIRECTLY over second base, how far does the baseball travel? The THOUSANDTHS digit is equal to D.
Problem #2: Joe is watching fireworks over the 4th of July weekend. He wants to know how high the fireworks explosions are off of the ground. Standing 315 feet away from the launch location on the ground and 350 feet away from the explosion in the sky, how high are the fireworks explosions from the ground? The HUNDREDTHS digit is equal to E.
Problem #3: Bob is geocaching at his nearby park. From his location, he can travel 100 feet forward, take a 90 degree turn to the right, travel 60 feet forward, and then arrive at the cache. But, he can also choose to bushwack a straight path to the cache. Find the bushwacking distance to the cache, and the THOUSANDTHS digit is equal to F.
Problem #4: How far from the base of a house do you need to place a 15 foot ladder so that it exactly reaches the top of a 12 foot tall wall? This answer is equal to G.
Problem #5: A flagpole, which was originally 81 feet tall, broke in a storm. 28 feet are still sticking straight out of the ground, where it snapped, but the remaining piece hinged over and touches the ground some distance away. How far away ist he end of the poly from the base of the pole along the ground? The TENS digit is equal to H.
Problem #6: Chris is playing a game of basketball. The regulation height of a basketball rim is 10 feet high. If he stands 7 feet away and shoots the ball off of the ground, how far will the basketball travel before he misses and hits the front of the rim? The ONES digit is equal to J.
To check your solution, CLICK HERE.