A "Mad Scientist" cache (#2)
Please NOTE: the above coordinates are Fake!
Once again, Professor Von Clumsen, faithful to his name, has misplaced one of his test tubes… Oh, my!
This time, in order to locate and retrieve it, he has decided to stay away from experiments and instead he set out to calculate the location mathematically. 
To this end, he has developed a highly sophisticated method, based on some interesting properties of a graph.
(Professor Von Clumsen is not famous for being a very practical person...)
Consider the following graph (Fig. 1), which extends indefinitely into the plane, i.e. it has an infinite number of nodes and edges.
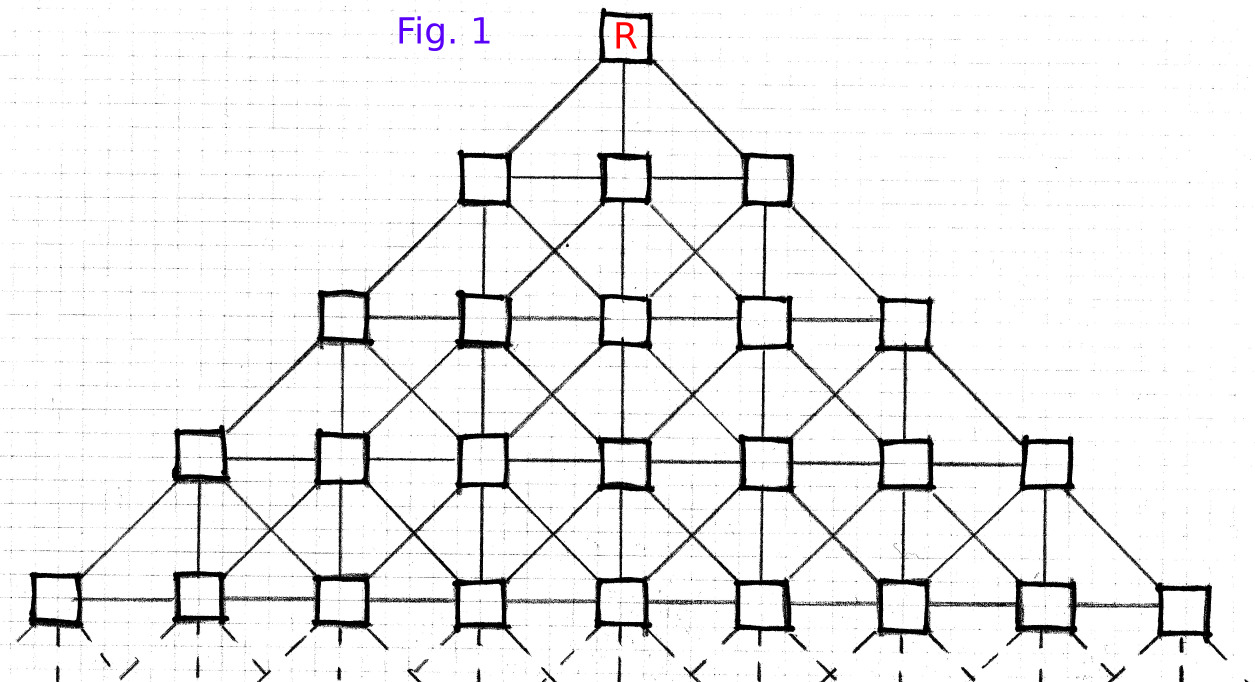
We say that the first node R is the root of the graph.
For each other node N we can then consider the distance d(N) from the root R: this distance is defined as the number of edges that one has to traverse in order to return back to the root R, starting from the node N, following an arbitrary path.
In general, for each node N there is an infinite number of such distances, due to the fact that there is an infinite number of paths that one can take to return to R from N, with some paths being longer than others.
Now consider only those paths that minimize the distance - in other words, only the shortest path(s) - and let’s call this minimum distance dmin(N)
The following picture (Fig. 2) might be helpful in fixing some of the concepts introduced above.
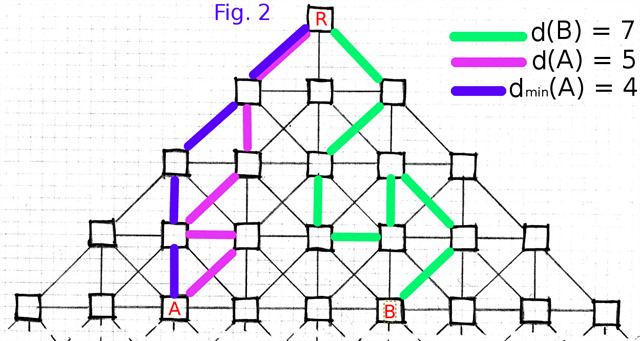
Next, let’s map the set of all positive integers onto the nodes of the graph, starting with 1 at the root, then proceeding to the second row, left to right, 2, 3, 4, then the third row, left to right 5, 6, … etc. ad infinitum
In this way every positive integer X corresponds to a node in the graph and we can talk about its distance dmin(X), which represents, as discussed above, the minimum number of edges that need to be traversed in order to return from the integer X all the way back to the root 1 at the top.
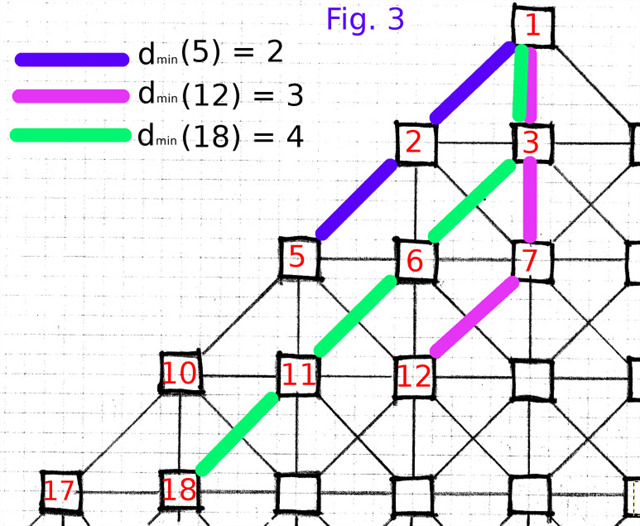
For example in the picture below (Fig. 3), dmin(5)=2, dmin(12)=3 and dmin(18)=4
Well, now that Professor Von Clumsen has formalized his theory, he is finally able to calculate the position of his lost test tube... but unfortunately he has also misplaced his pocket calculator!! Damn, he's truly incorrigible!
Can you help him find the coordinates?
North A° B.C
East D° E.F
where:

