spiromania #39
This is a puzzle cache. The cache is NOT located at the given coordinates. Rather it is located at
VK abcde fghij
which is short for UTM: 15T E 4abcde N 49fghij, as is usual in this series.
As Pi-Day (March 14) approaches it's only appropriate to have a Pi-based cache in this series. A Pi Spiral is a secondary spiral that results when an ordinary spiral is plotted point-wise using a large increment between the points.
Consider the Fermat spiral, given in polar coordinates by r =√θ, for 0 <= θ <= 2 π, shown in Figure 1 on the left above. It was plotted using 360 points, with an increment of one degree, i.e. inc = 1/360th of a revolution, between the points. If the increment is increased to inc = π revolutions we get the result shown in Figure 2 on the right above. Note the number of the Pi Spirals, emanating clockwise from the origin. Let a equal to that number.
For slightly different values of inc near π we can get very differently appearing spirals. Using inc = 3.0568, we get Figure 3 on the left below which shows a "Pi Flower", consisting of two interleaving sets of Pi Spirals - a clockwise set of 35 spirals and a counter-clockwise set of bc spirals. You can get a larger view by clicking on the magnifying glass icon. Inc = 3.18 yields Figure 4 on the right below, with de clockwise spirals. So far you should have the easting coordinate abcde. As a check you should get a+b+c+d+e = 18.
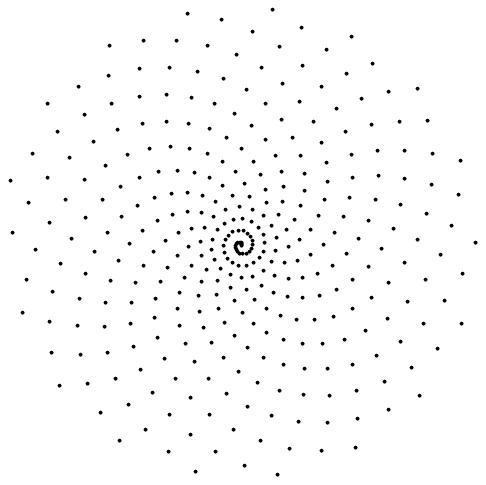 |
 |
To get f g h i j , we'll consider rational approximations, which are essential for an understanding of where the number of spirals comes from. Recall that a rational number is a real number that can be expressed as the ratio of two integers and an irrational number is one that cannot be so expressed. However, any irrational number x can be approximated arbitrarily closely by a rational number p/q, where p and q are integers. For a given number x and a given tolerance we're interested in the rational number p/q with the smallest denominator that approximates x within that tolerance. The well known approximation for π of 22/7 fills the bill for tolerances of 0.1 and .01. It's that denominator 7 that determined the number of spirals in Figure 1. The following table gives these approximations to π for tolerances from .1 to .000001.
| tolerance |
.1 |
.01 |
.001 |
.0001 |
.00001 |
.000001 |
| P/Q |
22/7 |
22/7 |
201/64 |
333/106 |
355/113 |
355/113 |
Now to get f g h i j, consider the rational approximations of √2 (= 1.414136 approximately). The first few are:
| tolerance |
.1 |
.01 |
.001 |
.0001 |
.00001 |
| P/Q |
3/f |
h7/12 |
j i/29 |
99/70 |
g77/408 |
Enter your solution into the coordinate checker in the form VKabcdefghij.
If correct you will provided the lat/lon coords and a hint on the hide.

You can validate your puzzle solution with certitude.
The first 10 solvers are:
1. PackADad Mon, 5 Mar 2018 21:11:19
2. ctc128 Mon, 5 Mar 2018 21:11:24
3. stolwood Mon, 5 Mar 2018 21:55:37
4. aliasmom Mon, 5 Mar 2018 23:29:26
5. rickrich Tue, 6 Mar 2018 11:45:07
6. foundinthewild Tue, 6 Mar 2018 16:47:47
7. turuthok Tue, 6 Mar 2018 18:11:39
8. salsman Sat, 10 Mar 2018 19:56:12
9. mnboyscout Mon, 12 Mar 2018 12:42:12
10. rohrerhj Wed, 11 Apr 2018 11:42:56
More than you need to know:
- The Fermat spiral was used because it's compact. Any Archimedian spiral will give similar results.
- Figure 2 doesn't tell the whole story of the Pi Spiral. If n, the number of points, is increased the 7 spirals fade away and are swamped by 64 spirals. Then if n is increased further we get 106 spirals. Etc. forever although the pictures aren't pretty.
- That real good approximation of 355/113 was discovered by the Chinese astronomer Tsu Ch'ung-Chih 1500 years ago, 1000 years before it was known in the west.
- As hinted at in the narrative, the spirals are extremely sensitive to the value of inc. The behavior is fractal, with many features appearing between any two values of inc.
- There's really nothing special about inc = Pi here. As you might expect you'll get similar results for √2 or any other irrational number. But Pi-Spirals and Pi-Flowers are the generic terms.
