
Klenkes means "pinkie". Erecting the little finger (not the middle one) of the right hand is the traditional token of the people from Aachen, the Öcher. It reminds us of the industry of needle production which had been widespread in the region for a long time. Defective needles were sorted out from the assembly line by a typical motion of that finger. This part of the production process was called "ausklinken" - hence the word of the local dialect for that part of the body. Many Öcher having been doing this all their life developed a typical deformity and could thus be recognized by their crippled finger. Today, many decades after the decline of the local cloth and needle industries, you can still happen - let's say: in Katmandu - to spot two people greeting each other by holding up the right hand and showing their pinkie. Don't fear for their health, but you will instantly know where they come from.
If you happen to pass by N 50 45.068 E 006 10.976 on Sunday, 2nd of September 2018, you will find some Öcher geocachers having a good time together and celebrating themselves and their hobby by an event - the Klenkes - held yearly and having also become traditional - as it has to publish some caches on the day of the event. -
I'm sorry, but until now, there is no English translation of the following tasks available.

Geometrische Knobeleien 2.5
Eigentlich sollte dieses Rätsel ganz anders aussehen, einfach nur "Geometrische Knobelei" heißen und lediglich eine Aufgabe umfassen. Inhaltlich sollte es an den klasse Mystery des Teams Bandweber zum Event des Jahres 2016 Klenkes 2016: Geometrische Knobeleien (GC6NYM8) anschließen. Selbstverständich kam auch nur das Team Bandweber als Beta-Tester in Frage. Doch als ich diesem das Roh-Listing zuschickte, bekam ich postwendend die Antwort, der Test sei in weniger als einer Minute zu erledigen: Meine Aufgabe sei in ihrer eigenen Fortsetzung [Klenkes 2018] - Geometrische Knobeleien (2) (GC7TMQP) enthalten. Nachdem ich zunächst überlegt hatte, die ganze Sache einzustampfen, habe ich mich nun doch entschlossen, an meinem Plagiat festzuhalten. Will sagen: Dass wir beide auf exakt dieselbe Rätselidee gestoßen waren, liegt natürlich daran, dass wir dieselbe Quelle genutzt haben. Aus dieser stammen denn auch folgende Knobeleien. Hoffentlich lassen sie sich - zumindest in Teamwork - ohne größere Probleme beim Grillen lösen.
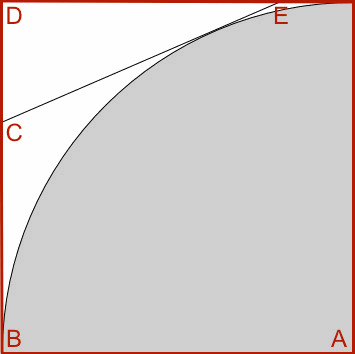
1.) Zuerst aber eine Anschlussaufgabe an Rätsel Nr. 2 von GC7TMQP:
a) Wie groß ist der Umfang des Dreiecks CDE?
b) Abhängig von der Lage der Punkte C und E auf der linken und oberen Kante des Quadrats lassen sich weitere Dreiecke konstruieren, bei denen CE tangential an der Viertelkreislinie anliegt. Wie groß ist der minimale Wert von CE?

2.) Als nächstes etwas Leichtes zum Aufgalopp: Ein Schilfrohr wächst vom Grund eines Teiches senkrecht nach oben und ragt sechs Ellen über die Wasseroberfläche hinaus. Plötzlich kommt ein starker Wind auf, der das Rohr an der Wurzel knickt, ohne es zu entwurzeln, so dass es so weit zur Seite treibt, dass seine Spitze nun genau auf Höhe des Wasserspiegels liegt, und zwar zwölf Ellen von der Stelle entfernt, wo es zuvor aus dem Wasser austrat. Wie lang ist das Rohr?

3.) Jetzt wird es etwas schwieriger: Insekten nutzen bekanntlich Sonne und Mond, um eine Flugrichtung in gerader Linie einzuhalten; sie machen sich dabei zunutze, dass die Strahlen dieser Lichtquellen parallel einfallen. Aber ihre erstaunliche Fähigkeit zur Orientierung im Raum wird etwa Faltern oder Motten zum Verhängnis, wenn sie in die Nähe einer Kerze geraten, deren Flamme ihre Lichtstrahlen radial aussendet. Eine Motte, die konstant einen spitzen Winkel von α Grad zu dem sie gerade treffenden Strahl einhält, wird so dazu gezwungen, sich der Flamme in spiralförmiger Bahn zu nähern, bis sie verzehrt wird.
Wie lange dauert der Flug einer Motte, die in einem Abstand von 6 m zur Flamme startet, einen konstanten Winkel von 60° zu dem sie jeweils treffenden Lichtstrahl einhält und mit einer konstanten Geschwindigkeit von 0,3 m/sek fliegt?

4.) Zum Abschluss eine Aufgabe für Fortgeschrittene und zugleich so recht eine für Geocacher: Ein reicher Kaufmann hatte keine Erben. Deshalb vergrub er seinen Nachlass, einen phantastischen Schatz, außerhalb seines Grundstücks nordöstlich des Brunnens vor seinem Gutshaus. Jener sollte sein würdiger Erbe sein, der die exakte Lage des Schatzes als erster berechnen oder ihn erreichen könnte. Dazu musste man vom Brunnen aus zunächst 1.000 Meter nach Osten gehen, danach im rechten Winkel nach links abbiegen und eine um 1/100 kürzere Strecke als die letzte in diese Richtung gehen, also 990 Meter nach Norden, dann wieder links und erneut eine um 1/100 kürzere Strecke, also 980,1 m, nach Westen, usw.
a) Wie viele Meter vom Ausgangspunkt, dem Brunnen, entfernt befand sich der Schatz?
b) In welchem Winkel (zum Norden) lag die Himmelsrichtung, in der sich der Schatz befand?
Berechnet die Lösungen bis auf insgesamt drei Stellen (ohne Rundung) und gebt die sechsmal drei Ziffern der Beträge ohne Komma und Zwischenraum in den Certitudes-Checker ein.
Beispiel: Wären die Lösungen ad 1a) 32,5 Längeneinheiten, ad 1b) 6,3895 Längeneinheiten und ad 2.) 11 Längenenheiten, wäre als Zeichenkombination insoweit"325638110" einzugeben.

Du kannst deine Rätsel-Lösung mit certitude überprüfen.
Es handelt sich um ein Naturschutzgebiet, die offiziellen Wege müssen und dürfen zu keiner Zeit verlassen werden.
