English version below
Endnu en Enigma-serie!? Ja, men denne er unik, fordi den handler om at bryde Enigma-kryptering og ikke bare at dekryptere.
Med en Enigma-maskine tænker jeg i bredeste forstand på en maskine med et antal roterer, en reflektor og eventuelt et plugboard. Et tegn krypteres ved at det bliver sendt igennem striben af roterer, som hver laver en simpel substitution (som fx Rot13) og derefter laver reflektoren en enkelt substitution, hvorefter tegnet sendes tilbage gennem rotorerne af en anden vej og hver rotors substitution foretages nu baglæns.
Det lyder indviklet, men det er faktisk ikke så slemt. Prøv at se dette simple eksempel med en rotor og en reflektor:
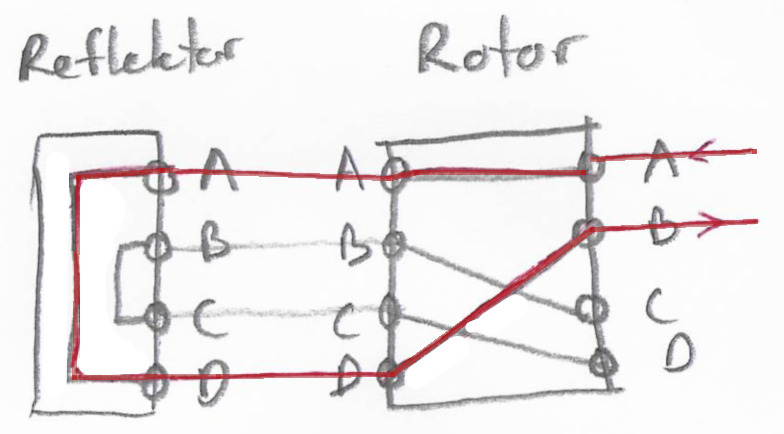
A → A (rotoren) → D (reflektoren) → B (rotoren på tilbagevejen)
Rotorens kryptering skrives ABCD → ADBC og reflektoren ABCD → DCBA.
Den næste figur viser kryptering af T i en historisk korrekt Enigma-maskine med plugboard, 4 rotorer og reflektor. Tilslut sendes signalet til en stribe små pære, hvor det krypterede bogstaver lyser op. Det statiske hjul til højre har ingen effekt matematisk set. Formålet er en ren mekanisk/elektrisk ”oversættelse” fra strøm i ledning til strøm et sted i et hjul.
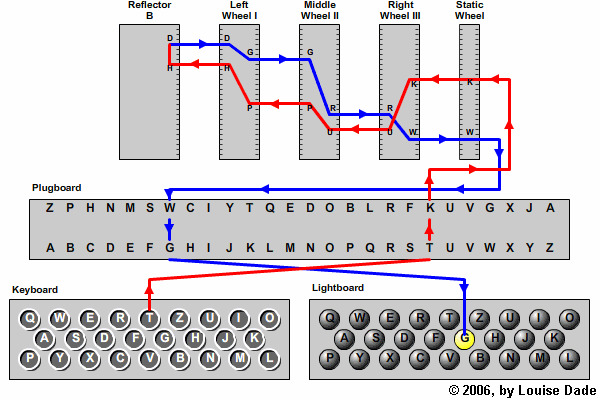
kilde: http://enigma.louisedade.co.uk/howitworks.html
Bogstaverne på lamperne korresponderer 1:1 med tasterne sådan, at hvis der ikke skete nogen kryptering vil alle bogstaver give sig selv (A→ A, B→ B, osv). Det har to meget vigtige konsekvenser: For det første vil alle bogstaver altid blive krypteret, dvs intet bogstav kan krypterer til sig selv. For det andet kan Enigma-maskinen bruges til både at kryptere og dekryptere. Disse to ting hænger nøje sammen. Hvis man bytter rundt på nogle af de små pærer så ryger begge egenskaber. (Tænk på det som at signalet er en strøm, der løber gennem maskinen uden kortslutninger).
Nu kommer vi til den indviklede del: Hver gang en tast trykkes ned kan en eller flere rotorer flytte en tak. Dette sker før krypteringen. Det betyder, at hvert bogstav krypteres med et nyt substitutionsalfabat. Helt præcist sker dette ved at indmaden af rotoren roterer en tak ned af. Bogstaverne på kanten bliver siddende.
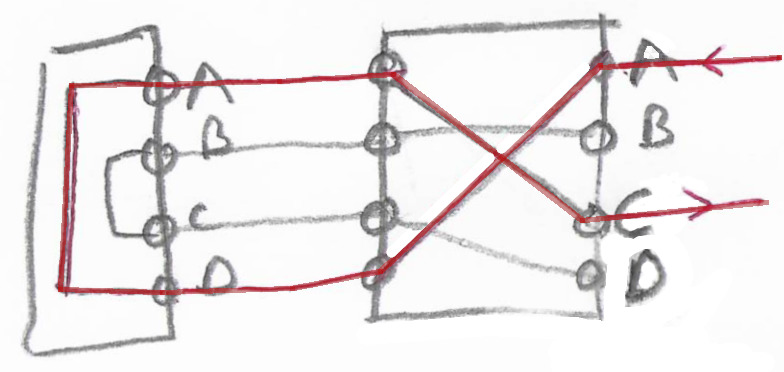
A → D (rotoren) → A (reflektoren) → C (rotoren på tilbagevejen)
Figuren viser stillingen i ABCD-engimaen efter at roteren har roteret og nu krypteres A → C. Læg for eksempel mærke til at den vandrette A-A forbindelse i den første figur nu er en B-B forbindelse.
Eksemplet er her er en mikro-Enigma, som er velegnet til at tegne diagrammer for på papir. Krypterer A nogensinde til D?
Endelig kan maskinen have et plugboard. Plugboardets funktion er at fortage en substitution mellem nogle af bogstaverne. Med de historiske 26 bogstaver kan man lave 13 substitutioner, men typisk blev der ikke brugt mere end 10. Dvs at 6 ( = 26 - 2*10) bogstaver bliver ikke krypteret af plugboardet. Plugboarded svarer til en roter, som ikke roterer, med fuld udskiftelig linjeføring.
For at finde denne cache skal du bryde krypteringen på min mini-Enigma. Det er ikke så svært som det lyder. Min mini-Enigma er så simple, som det kan lade sig gøre, uden at den er helt triviel.
Den har en rotor med 28 tegn, en reflektor og plugboardet har en forbindelse (en ledning forbinder to bogstaver). I grundstillingen foretager rotoren denne krypteringen
ABCDEFGHIJKLMNOPQRSTUVXYZÆØÅ ->
DBPEMGZALRNKØYTJXÆOÅFUHCQVSI
Og reflektoren:
ABCDEFGHIJKLMNOPQRSTUVXYZÆØÅ ->
OHVFMDXBÅNSTEJAUZØKLPCGÆQYRI
Sådan finde du cachen - klarteksten er på dansk:
ÅLNPS GÅJDR ØMYUH ÅBXUU OUKVQ GLTBÅ JVXZI SFTØZ FHAIE LDFLÅ KHÅDH IYZZÅ XZISF TØVPP VVIQG D
Kan opgaven løses uden programmering? Ja, her er reflektoren og rotoren i samme stil som Print din egen mini-Enigma (GC878KE), men husk at plugboardet ikke er med her:
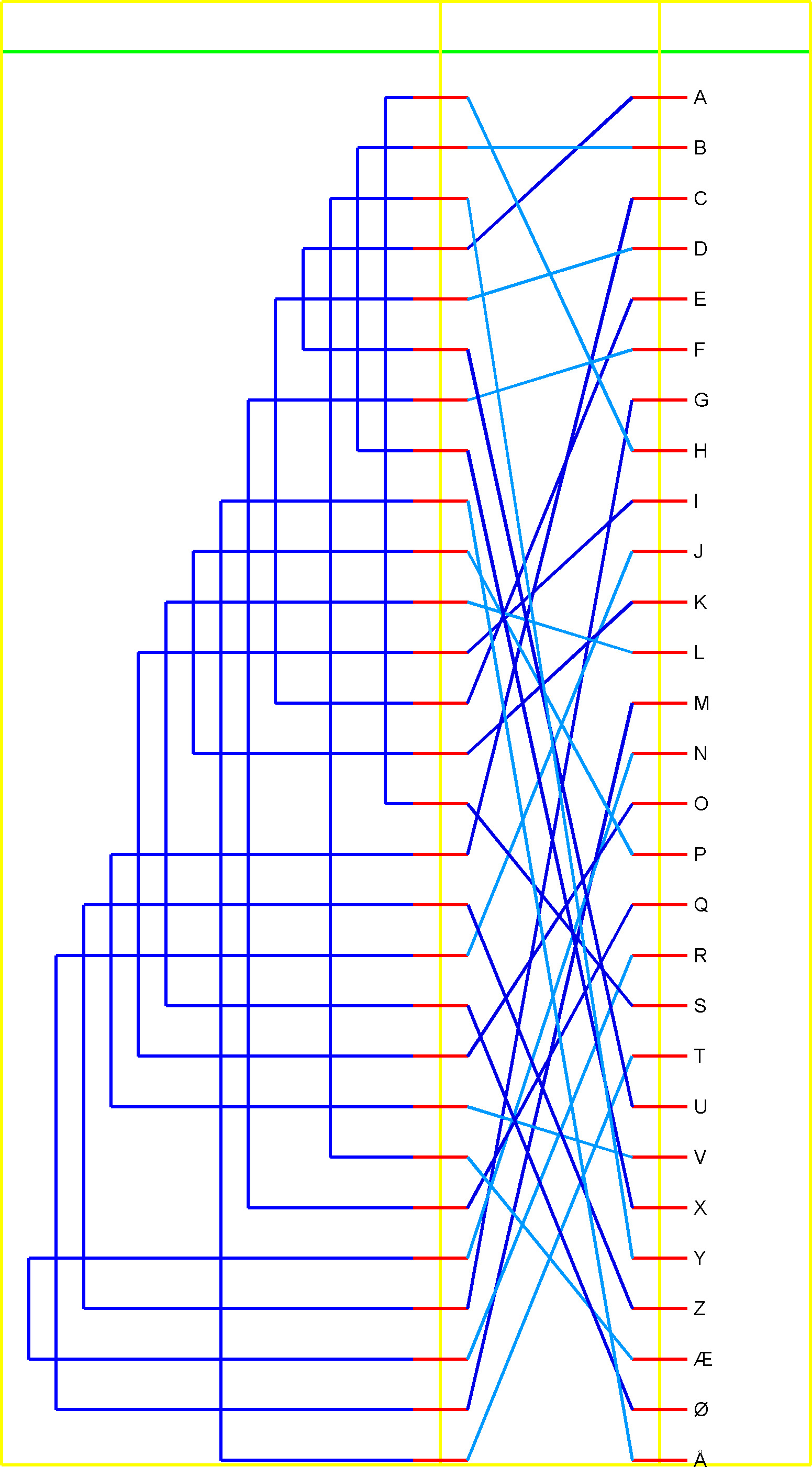
Cachen indeholder fra start - hold nu fast - FFC, JFFC, FTS (til første løser), SFFC (første senior) og DFFC (til første hund). (Kan man snart finde på flere?)
Jeg håber at dette kan blive den første cache i en serie, som udforsker Enigma-mekanismerne. Min tanke er at undgå maskiner, men præcis samme indmad som historiske Enigma-maskiner, fordi der findes en del software på nettet til at løse dem. Stort set alle Enigma-maskiner havde 26 tegn. En simpel ændring er at bruge 28. (27 eller 25 er en dårlig idé….. men hvorfor?)
Dette er ikke min serie - alle er velkommende til at tilføje dele.
Denne introduktionsopgave er både på dansk og engelsk. Fremtidige cacher forestiller jeg mig kun at lave på engelsk, fordi jeg ved at to ikke-danskere løser med. Hvis nogle ønsker dem på dansk også, så skriv.
Hvis du publicerer en cache langt væk fra Værløse-området, så læg et link i en write note på denne cache.
Angiv gerne sproget for klar-teksten. Det er måske ikke oplagt for løseren.
Inkl events og en lab cache er dette min cache nummer 100: 36 traditionele/multier/letterboxes, 5 events, 12 earth caches, 7 wherigos, 1 lab cache og 38 mysts. Af de 38 myst er fire kun blevet fundet to gange eller færre. Mine ’uløselige’ myster er altså 4% af mine udlagte cacher.
(20. marts 2019): To små tilføjelser:
På den historiske Enigma-maskine rotere ringen med bogstaver med, når rotoren roterer. De er ikke med i beskrivelsen.
Matematisk set er nemt at beskrive funktionen ved at give forbindelserne mellem rotorene bogstavsnavne, lige som her: Wikipedia: Enigma rotor details. Det gør blandt andet at man kan beskrive rotoresn effekt meget kompakt, som fx den historiske rotor VI Naval Enigma ABCDEFGHIJKLMNOPQRSTUVWXYZ → JPGVOUMFYQBENHZRDKASXLICTW
I 1925 blev fremstillet en Svensk Enigma B med 28 bogstaver A-Ö.
Yet another Enigma series !? Yes, but this one is unique because it is about breaking Enigma encryption and not just decrypting.
I use “Enigma machine” in the broadest sense. A machine with a number of rotates, a reflector and possibly a plugboard. A character is encrypted by being passed through the row of rotors, each making a simple substitution (such as Rot13) and then the reflector makes a single substitution, after which the character is sent back through the rotors backwards, and each rotor's substitution is now made backwards.
It sounds a bit complicated, but it's actually not that bad. Try this simple example with a rotor and a reflector:
A → A (the rotor) → D (the reflector) → B (the rotor on the return path)
The rotor encryption is written ABCD → ADBC and the reflector ABCD → DCBA.
The next figure shows encryption of T in a historically correct Enigma machine with plugboard, 4 rotors and a reflector. After encryption the signal is send to rows of small bulb, where the encrypted letters light up. The static wheel on the right has no mathematical effect. The purpose is a pure mechanical / electrical "translation" from current in wire to current somewhere in a wheel.
Source: http://enigma.louisedade.co.uk/howitworks.html
The letters on the lamps correspond to 1:1 with the keys such that if no encryption occurs, all letters will give themselves (A → A, B → B, etc.). This has two very important consequences: First, all letters will always be encrypted, ie no letter can encrypt to itself. Second, the Enigma machine can be used to both encrypt and decrypt. These two things are closely linked. If you change some of the small bulbs then both properties will go. (Think of it as the signal is a current that runs through the machine without shorts).
Now we come to the intricate part: Each time a key is pressed one or more rotors can move one notch. This happens before the encryption. This means that each letter is encrypted with a new substitution alphabet. To be precise: A rotor rotates by the inside of the rotor rotating a notch down. The letters on the edge remains.
A → D (the rotor) → A (the reflector) → C (the rotor on the return path)
The figure shows the position of the ABCD Engima after the rotor has rotated and is now encrypted A → C. For example, note that the horizontal A-A connection in the first figure is now a B-B connection.
The example here is a micro-Enigma that is suitable for drawing diagrams on paper. Does A ever encrypt to D?
Finally, the machine can have a plugboard. The function of the plugboard is to make a substitution between some of the letters. With the historical 26 letters one can make 13 substitutions, but typically no more than 10 was used. That is, 6 (= 26 - 2 * 10) letters are not encrypted by the plugboard. The plugboard is similar to a non-rotating rotor with fully interchangeable connections.
To find this cache, break the encryption on my mini-Enigma. It's not as difficult as it sounds. My mini-Enigma is as simple as it is possible without it being completely trivial.
It has a 28-character rotor, a reflector and the plugboard has one connection (one wire connects two letters). In the basic position, the rotor makes this encryption
ABCDEFGHIJKLMNOPQRSTUVXYZÆØÅ ->
DBPEMGZALRNKØYTJXÆOÅFUHCQVSI
And the reflector:
ABCDEFGHIJKLMNOPQRSTUVXYZÆØÅ ->
OHVFMDXBÅNSTEJAUZØKLPCGÆQYRI
How to find the cache - the plain text is in English (with “W” substituted by “V”):
ÅLNPS SDAHØ GZFDP KTGIØ HBKLI LLZÆB UYQGX ØBRVZ ÅSDXB RIÅLÅ HHGPX IEFÅD LZJBS HHMÆZ OXEQE XIÅCM I
Can it be solved without programming? Yes, here is the feflector and rotor in the same style as Print din egen mini-Enigma (GC878KE). Remeber that the plug board is not in the diagram:
The cache contains from the start - FFC, JFFC, FTS (for first solver), SFFC (first senior) and DFFC (for first dog).
I hope this can be the first cache in a series that explores the Enigma mechanisms. My idea is to avoid machines, identical to historic Enigma machines, because there are a lot of software on the web to crack them. Almost all historical Enigma machines had 26 characters. A simple change is to use 28. (27 or 25 is a bad idea… but why?)
This is not my series - everyone is welcome to add caches.
If you publish a cache far from the Værløse area, please put a link in a write note on this cache.
Also maybe specify the language of the clear text. Maybe it is not obvious for the solver.
This is (including events and a lab cache) my cache number 100.