¡¡Bonus caché de la serie Cachés por Vallecas: Sucesiones!!
En vez de realizar un bonus normal y corriente, quería hacer algo diferente, por lo que el Caché bonus está dedicado a las sucesiones y a la resolución de varios ejemplos prácticos.
Sucesiones
Una sucesión es una serie de elementos, finita o infinita, que se siguen unos detrás de los otros en el tiempo o en el espacio atendiendo un orden.
Sucesión viene del latín succsessio compuesto por el prefijo sub- que indica ‘debajo’, cessus que se refiere al ‘acto de andar’ o ‘marchar’ y el sufijo -io que indica acción. Por lo tanto, sucesión significa la acción y efecto de seguir un camino ya trazado, en este caso, por números.
Sin duda, la más conocida de las sucesiones es la sucesión de Fibonacci, que hace referencia a la secuencia ordenada de números descrita por Leonardo de Pisa, matemático italiano del siglo XIII y que ha sido citada y utilizada en varias novelas, como en "El código da Vinci" o en el libro “Crónicas de la última revolución” donde se numeran los capítulos precisamente con los números de la sucesión de Fibonacci, desde el 1 hasta el 89.
La curiosa serie tan interesante es la siguiente:
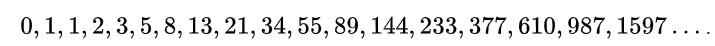
Pero hay muchas más sucesiones no tan conocidas por el resto de los mortales, como las que se mencionan a continuación:
- Sucesión de Farey: Es una sucesión matemática de fracciones irreductibles entre 0 y 1 que tienen un denominador menor o igual a "n" en orden creciente. Cada sucesión de farey comienza en el 0, denotado por la fracción 0/1 , y termina en el 1, denotado por la fracción 1/1 , aunque algunos autores suelen omitir ambos términos. La sucesión de Farey para n entre 1 y 8 es la siguiente:
Sucesión de Hofstadter: Es una familia de sucesiones de números enteros relacionadas entre sí y definidas por relaciones de recurrencias no lineales. Estas sucesiones son más complicadas y dentro de ellas, hay una cosa muy curiosa y es que se llegan a definir sucesiones masculinas y femeninas. Siendo los primeros términos de la serie los siguientes:
Femenina: 1, 1, 2, 2, 3, 3, 4, 5, 5, 6, 6, 7, 8, 8, 9, 9, 10, 11, 11, 12, 13...
Masculina: 0, 0, 1, 2, 2, 3, 4, 4, 5, 6, 6, 7, 7, 8, 9, 9, 10, 1, 1, 12, 12...
Hay muchas más sucesiones, mucho más complicadas, como la sucesión de Goodstein, Cauchy...que tienen expresiones mucho más complejas ya que emplean límites de sucesiones convergentes con largas expresiones matemáticas, por lo que no se va a entrar en detalle en esas. En
En cambio, en vez de tratar de comprender esas sucesiones tan complicadas, para averiguar en qué cachés de la serie se encuentran los valores necesarios para hallar las coordenadas finales del bonus, tendréis que averiguar los números que faltan en las siguientes sucesiones:
A) 1,A,B,4,7,11,16,H,29...
B) G,F,13,21,29,25,21...
C) C,9,D,11,10,13,12,E,14,17,16,19...
Estos números se corresponden con los números de los cachés de la serie en los que tendréis que buscar y anotar un valor. Finalmente, una vez que hayáis obtenido esos valores, tendréis que poner sus variables (letras) en el orden numérico ascendente e introducirlos en el siguiente certitude:
Sobre el caché:
Este es un caché muy especial que también teníamos ganas de colocar desde hacía tiempo. Último caché escondido del año, colocado dos días antes de que acabe el año con ayuda de mukad. Os deseo a todos una feliz entrada y salida de año!
Me gustaría daros más información acerca del caché, pero no os quiero desvelar nada. A ver qué os parece la idea del caché...solo puedo desearos mucha suerte y espero que disfrutéis tanto o más como yo lo he hecho, ideando y colocando el caché.
Dejo un par de TBs para intercambiar.
Lleva preparado un mes, pero debido a la nevada, la falta de tiempo y la necesidad de realizar el mantenimiento a unos cuantos cachés de la serie, hemos tenido que esperar un poco más hasta la publicacion del mismo, pero aquí está, espero que os guste!
Tal y como pone en los atributos del caché, es muy recomendable realizar el trabajo en equipo para hacer la experiencia más divertida.
Cuando lo encontréis dejarlo tal y como estaba!
Prácticamente todos los cachés son caseros, así que, tener cuidado a la hora de manipularlos.
Suerte y feliz geocaching!
