|
![]() 
|
Platonic solid:
Any of the five geometric solids whose faces are all identical, regular polygons meeting at the same three-dimensional angles. Also known as the five regular polyhedra, they consist of the tetrahedron (or pyramid), cube, octahedron, dodecahedron, and icosahedron. Pythagoras (c. 580–c. 500 BC) probably knew the tetrahedron, cube, and dodecahedron. According to Euclid (fl. c. 300 BC), the octahedron and icosahedron were first discussed by the Athenian mathematician Theaetetus (c. 417–369 BC). However, the entire group of regular polyhedra owes its popular name to the great Athenian philosopher Plato (428/427–348/347 BC), who in his dialogue Timaeus associated them with the four basic elements—fire, air, water, and earth—that he supposed to form all matter through their combinations. Plato assigned the tetrahedron, with its sharp points and edges, to the element fire; the cube, with its four-square regularity, to earth; and the other solids concocted from triangles (the octahedron and the icosahedron) to air and water, respectively. The one remaining regular polyhedra, the dodecahedron, with 12 pentagonal faces, Plato assigned to the heavens with its 12 constellations. Because of Plato’s systematic development of a theory of the universe based on the five regular polyhedra, they became known as the Platonic solids.
Euclid devoted the last book of the Elements to the regular polyhedra, which thus serve as so many capstones to his geometry. In particular, his is the first known proof that exactly five regular polyhedra exist. Almost 2,000 years later the astronomer Johannes Kepler (1571–1630) resuscitated the idea of using the Platonic solids to explain the geometry of the universe in his first model of the cosmos. The symmetry, structural integrity, and beauty of these solids have inspired architects, artists, and artisans from ancient Egypt to the present. |
| The Platonic Solids: |
|

|
Tetrahedron:
faces=4, edges=6, vertices=4 |
![]()  |
Cube:
faces=6, edges=12, vertices=8 |
 |
Octahedron:
faces=8, edges=12, vertices=6 |
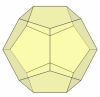 |
Dodecahedron:
faces=12, edges=30, vertices=20 |
 |
Icosahedron:
faces=20, edges=30, vertices=12 |
|
The Nesting Pairs: As Illustrated in the larger image, at the top of the page.
These five solids fit into one another as follows: |
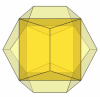 |
Cube / Dodecahedron:
The 8 vertices of the cube align with 8 of 12 of the vertices of the dodecahedron. Each face of the dodecahedron has an edge of the cube running along it's face. |
 |
Tetrahedron / Cube:
The four vertices of the tetrahedron align with 4 of the 8 vertices of the cube. Each face of the cube has an edge of the tetrahedron running along it's face. |
 |
Octahedron / Tetrahedron:
Each of the 6 vertices of the octahedron align with the center of each edge of the tetrahedron |
 |
Icosahedron / Octahedron:
8 of the 20 faces of the icosahedron sit flat against each of the 8 faces of the octahedron. |
| |
The Problem:
As you can see by the provided imagery, each of the Platonic solids fit perfectly inside of one another. Given that the surface area of the icosahedron is 3.307, determine the shortest, and longest possible distance between any vertex on the icosahedron, and any vertex on the dodecahedron. round to thousandths. Subtract the shortest distance from the posted latitude, And add 1/2 of the longest distance to the posted longitude. |
|
|

|
| |
Important: read this:
It is possible to inscribe the icosahedron within the octahedron two different ways which vary only in their rotation or "handedness.". The rotation pictured in the imagery will lead to 8 identical sets of 12 lengths per set, plus another 12 identical sets of 12 lengths each. Using the other rotation to inscribe the icosahedron, will result in your outcome containing 20 identical sets of 12 lengths each, and will not result in the longest/ shortest length possible. |
Thank You! to RS, whose knowledge on the subject
was crucial to bringing this one to fruition!
|