DON'T PANIC
1. Yes, the first nine caches in the PS101 Series have been archived.
2. I took the Final Exam clue out of the cache container and hid it online here.
3. The Final Exam is still alive and ready for you to find.
The first nine caches in this series had themes and solutions directly related to the locations where they were hidden. Since they were first hidden in 2007, some of those locations changed considerably - in one case, the original hiding spot completely disappeared.
If you're thinking of starting PS101 or have already begun and collected some of the clues, fear not! The puzzles and clues for the first nine caches are all available online here.
If you're a past, present, or future Remote Solver, there's an added bonus for you: all of the clues that once existed only in the physical containers are now online. You can now collect the clues and solve the final puzzle of The Final Exam.
About This Series
The first nine caches in this series will help you build your puzzle-solving skills. Each one contains a lesson focusing on a specific skill, examples of how to use that skill, an exercise to test that skill, and a cache to find as a reward. Study the lesson, complete the exercise, and you'll find the location of a geocache.
Each of those caches contains a piece of information you'll need to take the final exam (the tenth cache in the series). Bring some way of recording those clues for later ... paper and pen/pencil would come in handy, or perhaps a camera. (A hammer, chisel, and very large rock would work but probably wouldn't be very handy.)
Lesson 6: Logic Problems
Introduction
Logic problems test your deductive reasoning skills. They challenge you to take a bunch of pieces of information and to make logical inferences from them. Academic as this sounds, they're a lot of fun.
This a lengthy lesson, but it's an important one. Logic problem solving skills are required to solve a variety of puzzles ... wordplay, mathematics, cryptography, lateral thinking, and other types of puzzles incorporate many aspects of logic problems. The skills in this lesson are some of the most universally applicable in this series.
What Is a Logic Problem?
A traditional logic problem deals with a set of objects (such as people or houses) that share a set of properties (such as occupations or colors). Each of the objects usually has a unique value of each property (ie, there's only one farmer or one blue house). You are given a set of true statements about the objects and their properties - from those statements, it is your job to figure out the value of each property of each object in the puzzle.
Logic puzzles often provide you with a solution grid to fill in as you analyze the clues. The grid shows all possible combinations of all values of all properties. See the exercise below for an example of what a grid might look like. (Evil puzzle constructors sometimes conveniently forget to supply you with the solution grid.)
To solve the puzzle, you must populate the grid with information. I usually mark the things that I know are true with a dot, and the things that I know are false with an X. When you have filled in the entire grid with dots and Xs, you're done.
Types of Clues
A positive clue makes an explicit association between two parts of the puzzle. For instance, if you had a puzzle that required you to figure out what color kilts a bunch of clans wore to a feast, a positive clue for that puzzle might be: The 4 Dogs wore lovely rubicund kilts the night of the feast. In the puzzle grid, you can put a dot in the cell where The 4 Dogs and rubicund kilts meet since you know that to be true. You can also put an X in every other color kilt for The 4 Dogs, and you can put an X in every other clan for the rubicund kilts.
A negative clue says explicitly or implicitly that two parts of the puzzle are not related. For instance, suppose you have this clue: The Romulan Cabinet Ministers sat across the table from the clan in the indigo kilts. You know right away that there is no possible way that the Romulans could be wearing indigo, so you can put an X in the grid cell that relates the two. (Besides, everyone already knows that Romulans would never wear indigo under any circumstances.)
A relative clue expresses some kind of ordered relationship between puzzle elements. For example: The clan in indigo kilts ate less than the clan in the fuchsia kilts, but the clan in the ochre kilts ate less than the clan in the indigo kilts. You now know:
ochre < indigo < fuchsia
If you have a list of amounts that each clan ate, then you know right away that fuschia cannot be the smallest or next smallest values - if it was, there would be no valid way to fit ochre into the puzzle. By the same logic, you know that the ochre cannot have the largest or next largest value, and you know that indigo cannot have the largest or smallest values. You can put an X in each of those cells in the grid.
An implied clue gives you indirect information about the solution, possibly referring to information that isn't in the grid and may not be explicitly stated in the puzzle. For instance, consider this clue: The number of pies eaten by the David Copperfield Worship Society is equal to the third prime number. You'd have to go figure out or look up the prime numbers, where you'd discover that the DCWS ate five pies.
A single clue may have multiple types of information. For instance, consider this clue: The Romulans ate more pies than the clan in chartreuse kilts, who ate more pies than the clan that ate 17 pies. You can infer that the Romulans are not wearing chartreuse, the chartreuse clan didn't eat 17 pies, and the Romulans didn't eat 17 pies. And the Romulans and the chartreuse clan didn't eat any fewer than 17 pies. So you can place X marks in all of those cells in the grid.
Solving Techniques
Use a Pencil
Don't use a pen. You will mess up. You will erase. You will erase a lot. Trust me on this one; you'll thank me later.
Start with the Obvious
Take a first pass through all of the clues, and record the facts that are immediately apparent.
Eliminate All But One
If you find a row or column in a block of your grid that has an X in every cell except for one, then you know right away that cell must have a dot in it. Place a dot in that cell, then place Xs in the rest of the dot's row and column in that block. As you fill in more of the grid, you may find that doing this once will trigger a chain of iterations of filling in dots and Xs.
Substitution
Once you know that two parts of the puzzle are related, you can replace all instances of one of those parts with the other. For instance, if you know the Romulans are wearing fuchsia kilts, go through the clues again and replace the phrase "Romulan Cabinet Ministers" with "clan wearing fuchsia", then see what that tells you. Then do it again and replace "clan wearing fuchsia" with "Romulan Cabinet Ministers", again looking for new information.
Inferences
An inference is something you deduce logically to be true, based upon other true statements. For instance, if your grid says that the Romulans are wearing fuchsia kilts and the clan wearing fuchsia ate 23 pies, then you can safely infer that the Romulans ate 23 pies. You can then mark that combination as true in your grid and carry on. That inference can then be used to draw more inferences and fill out more of the grid.
Hypothesis Testing
Sometimes when solving logic problems, especially more difficult ones, you run out of immediately obvious information. You can get to a point where you haven't finished the grid, yet you don't have any more information to add. Your only choice is to guess.
Mark your guess in the grid in some special way - use a different set of symbols (such as circle and square instead of dot and X, or use a different color pencil (because there's no possible way you'd be using a pen, right?)). Pick one cell and mark it as true or false, then see where it leads.
If you end up solving the puzzle, your guess was correct. But you may end up with a contradiction - for instance, you might find that your guess implies that both the Romulans and the David Copperfield Worship Society are wearing rubicund kilts. Since that can't be true, your guess was wrong ... and you have to backtrack. Erase all of the marks you made as a result of the guess (you didn't use pen for this, did you?).
Since your guess led to a contradiction, you now know that the opposite of your guess must be true. If your guess was to put an X in a particular cell and that guess led to a contradiction, you can safely replace that X with a dot.
Brute Force
This is exactly what it says. Sometimes you get to a point where you're completely out of ideas, but you only have a small number of possibilities left. When you started the puzzle, it would have taken too long to guess all possible combinations of values, but if you only have a few values left, you might be able to start guessing.
Brute force guessing means that you test all possible remaining combinations of values to see if that combination works. If that combination doesn't work, then move on to the next combination.
Check Your Work
There's nothing more infurating to finish a logic problem, look up the solution, and discover that you made a mistake somewhere. Fortunately, there's an easy way to avoid that situation.
When you complete the puzzle, go back and check whether the statements you're given are true. If you've done the puzzle correctly, every single one should be true. If you find a statement that isn't true, you've made a mistake along the way. Chances are that you'll have to erase and start over again (if you did the puzzle in pencil) or throw the puzzle away (if you did the puzzle in pen). (Have I mentioned to you that trying to solve one of these puzzles with a pen is a bad idea?)
Other Types of Logic Problems
Logic problems come in many, many different forms - listed below are some examples using numbers, letters, or pictures. The solving techniques described above apply equally well to all of them.
Sudoku
Surely you've heard of this craze that's swept the nation and the world over the past few years. All of the techniques given above for traditional logic problems work equally well for sudoku.
A sudoku isn't a math problem, it's a logic problem. You could solve a sudoku with letters of the alphabet or funky font symbols instead of numbers.
To solve a sudoku, I typically go through each square and write all of the numbers that could be in that square (that aren't already in the same row, column, and box). Once I get through the entire puzzle, I go back and look at what I wrote - if a number appears only once in a row, column, or block, then that number has to be in that cell.
Word Fill-Ins
A word fill-in isn't a word problem, it's a logic problem that just so happens to use words. A crossword-like framework is given along with a list of words - your job is to put them all in the framework so that each word is used exactly once and each cell is filled with exactly one letter.
You can solve a fill-in in a language you don't speak - it's just a matter of finding a way to fit the words into the given spaces.
Paint By Numbers (aka Nonogram)
A paint by numbers puzzle consists of a grid with various numbers across the top and down one side. The numbers in each row or column tell you three things: how many groups of colored cells there are in that row or column, how long each group is, and in what order they appear. When you've finished deducing which squares are colored and which ones are empty, you'll end up with a picture that looks like it came from an 8-bit black-and-white video game.
They're great puzzles, but describing them in text doesn't do justice to them. Wikipedia has a much better article on them, including animated illustrations to demonstrate their solution.
Additional Resources
As always, Google has lots of excellent hits for sites, such as this one, that can help you solve logic problems.
There are even automated sudoku solvers, but using one will cause you to suffer a lifetime of guilt and shame.
Exercise 6: Smorgasbord Game
I love board games and card games. I just wish I had more time to play and more people with whom to play and more games to play. All of the games listed in this exercise are in the game cabinet at home.
Five friends have just come out of a board game shop, and each has purchased his or her favorite board game. The five friends are: Alice, Bob, Carl, Daniel, and Emily. The five games they purchased are: Cranium, GoLo, Mille Bornes, Settlers of Catan, and Waterworks. Each game costs a different amount, and each game has been rated differently on a scale of 0 (worst) through 10 (best) by the readers of BoardGameGeek.com.
Each of these game sets may include dice, cards, or both (plus a board, tokens, card trays, roads, settlements, clay, golden wrenches, and other trinkets that don't matter for the sake of this puzzle). If you don't know which game is played with what items, the links above should help you figure that out.
Note: A Cranium set includes only a single die. Having to say "a die or dice" over and over again is going to be as tough for me to write as it is for you to read, so for simplicity's sake just pretend that Cranium is played with more than one die.
Using the following statements, determine what each friend's favorite game is, how much it costs, and what its BoardGameGeek.com rating is.
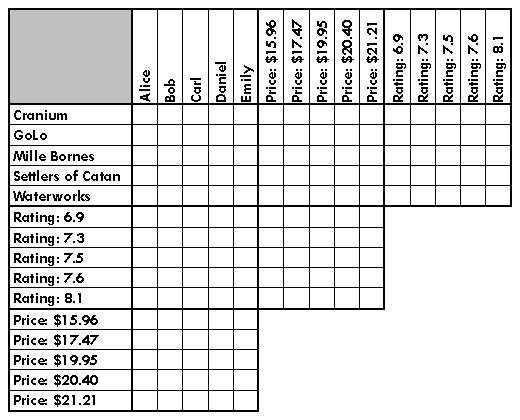
- Bob's favorite game costs less than Waterworks, which costs less than the game with the 7.6 rating.
- Mille Bornes is rated higher than the game that costs $19.95, which is rated higher than Carl's favorite game.
- The friend who paid $15.96 for his game got a real deal since his game has an 8.1 rating.
- Daniel's favorite game isn't the top rated, but it also didn't cost the most.
- Neither the most expensive game nor the worst rated game are played with dice.
- Carl's favorite game costs more than Settlers of Catan, which costs more than the game with the 7.5 rating.
- The game that costs $19.95 (which is not Emily's favorite) is not rated 7.5.
- The game that costs $17.47 uses dice but not cards, unlike the game with the 7.6 rating which uses cards but not dice.
- The person whose favorite game is rated 7.5 is male.
| Friend |
Favorite Game |
Game Price |
BGG Rating |
Value
(Price * Rating) |
| Alice |
|
|
|
|
| Bob |
|
|
|
|
| Carl |
|
|
|
|
| Daniel |
|
|
|
|
| Emily |
|
|
|
|
Once you've solved this puzzle, you're not quite through. For each friend's game, multiply the game's price by its rating to get its "value" (for lack of a better term). Plug the appropriate values into the following equations to find the final location of this cache.
| North Minutes = Alice's game's value - Cranium's value |
| West Minutes = Emily's game's value - Settlers of Catan's value |

For a real logic (and endurance) challenge, go find Let the Games Begin!
PS: If you're considering hosting a board game geocaching event, let me know where, when, and what I can do to help make it happen.