Multilateral Substitution Ciphers with Superencipherment
The first cipher we looked at, Cipher Tin, was the simple substitution cipher. The second, Cipher Bronze was a Dinome.
The third, Cipher Silver was a mixed Monoliteral-Biliteral..
All of these can be easily solved and are not very secure. However, just one more small step and they become one of the strongest of classical ciphers and were used up till the 1950's.
The term 'superencipherment' means adding additional layers of complexity to the enciphering process. Up until now we have been able to convert the cipher to a standard substitution cipher and then solve it using classical frequency count methods of either a monome or a dinome. But what we really need to do is ensure that this step can not be achieved by effectively converting it to polyalphabetic cipher, one in which each plaintext letter can be changed to many values.
This type of cipher is also called a "checkerboard cipher".
First we create the cipher table as shown below. Note that the 2 columns not used on the first row form the row numbers on row 2 and 3. In this case we have left blank the 2 and 6 on the first row.
Furthermore the first row contains the 8 most common letters, highest frequency first, with the rest of the alphabet put in in ascending order.
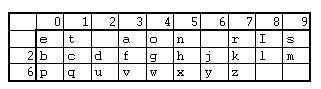
The key to what we have done here is the 2 digit number, in this case '26'
For the super-encipherment stage we choose a keyword and convert it to numbers using the table.
e.g. "cache" becomes '21321250'
We then convert the plaintext message in the same way we have done in previous Cipher Series caches:
pt: "this is the message"
ct: 12589891250290993240
but now we add, without carrying, the keyword digits:
ct: 1 2 5 8 9 8 9 1 2 5 0 2 9 0 9 9 3 2 4 0
+ : 2 1 3 2 1 2 5 0 2 1 3 2 1 2 5 0 2 1 3 2
-------------------------------------------
3 3 8 0 0 0 4 1 4 6 3 4 0 2 4 9 5 3 7 2
These can now be converted back to text, repeating the last digit if required:
A A I E E EO T O V O E G S N A R D
As can be seen repeated letters are now gone and deciphering is now very difficult, particularly with short plaintext.
Cracking Multiliteral Substitution Ciphers
Cracking this really isn't fun and is extremely difficult without multiple or long ciphertexts.
You are welcome to try but when this fails please resort to this crossword style clue to build the cipher table and determine the keyword:
"At the initial location can be seen a (4,6)"
The first word has a unique number associated with it you will need to replace 26.
When you have the table, the ciphertext can be run through above enciphering sequence in reverse to get the final cache location in plaintext.
The Cipher for the "Cipher Gold" location is:
TROSN ARNER TNOOO IARLS ERREN
PTEIS GHTOS NARSB OIEAO SITIN
REJNO OFTEN SNTRI EJNER ANSEX
SBETI BTLAR OPAOE XTRGA VRTAO
IT
btw, the keyword isn't "cache" nor the keycode "26".
As usual beware of muggles watching from the park to the north.